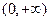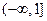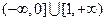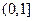题目内容
(本小题满分12分)
已知函数f(x)=2x的定义域是[0,3],设g(x)=f(2x)-f(x+2).
(1)求g(x)的解析式及定义域;
(2)求函数g(x)的最大值和最小值.
已知函数f(x)=2x的定义域是[0,3],设g(x)=f(2x)-f(x+2).
(1)求g(x)的解析式及定义域;
(2)求函数g(x)的最大值和最小值.
(1) g(x)的定义域为{x|0≤x≤1}
(2) -3
解:(1)∵f(x)=2x,∴g(x)=f(2x)-f(x+2)=22x-2x+2。 (3')
因为f(x)的定义域是[0,3],所以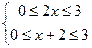 ,解之得0≤x≤1。
,解之得0≤x≤1。
于是 g(x)的定义域为{x|0≤x≤1}。(或写成[0,1],否则扣1分) (6')
(2)设g(x)=(2x)2-4×2x=(2x-2)2-4。 (8')
∵x∈[0,1],即2x∈[1,2],∴当2x=2即x=1时,g(x)取得最小值-4; (10')
当2x=1即x=0时,g(x)取得最大值-3。 (12')
因为f(x)的定义域是[0,3],所以
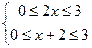 ,解之得0≤x≤1。
,解之得0≤x≤1。于是 g(x)的定义域为{x|0≤x≤1}。(或写成[0,1],否则扣1分) (6')
(2)设g(x)=(2x)2-4×2x=(2x-2)2-4。 (8')
∵x∈[0,1],即2x∈[1,2],∴当2x=2即x=1时,g(x)取得最小值-4; (10')
当2x=1即x=0时,g(x)取得最大值-3。 (12')

练习册系列答案
相关题目
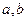 都有
都有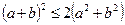 恒成立,则函数
恒成立,则函数
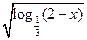 的定义
的定义 域为 ▲ .
域为 ▲ .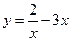 的最小值是 ★
的最小值是 ★ 


 有一个根位于下列哪个区间 ▲
有一个根位于下列哪个区间 ▲  ②.
②.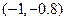 ③.
③.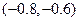 ④.
④.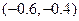
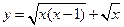 的定义域为( )
的定义域为( )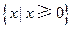
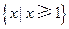
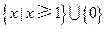
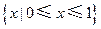
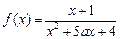 的定义域为R,则实数
的定义域为R,则实数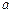 的取值范围是 ▲ .
的取值范围是 ▲ . 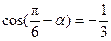 ,则
,则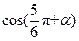 =___
=___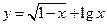 的定义域为
的定义域为