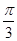题目内容
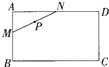 如图,长方形ABCD的长AD=2x,宽AB=x(x≥1),线段MN的长度为1,端点M、N在长方形ABCD的四边上滑动,当M、N沿长方形的四边滑动一周时,线段MN的中点P所形成的轨迹为G,记G的周长与G围成的面积数值的差为y,则函数y=f(x)的图象大致为( )
如图,长方形ABCD的长AD=2x,宽AB=x(x≥1),线段MN的长度为1,端点M、N在长方形ABCD的四边上滑动,当M、N沿长方形的四边滑动一周时,线段MN的中点P所形成的轨迹为G,记G的周长与G围成的面积数值的差为y,则函数y=f(x)的图象大致为( )A、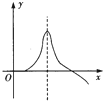 | B、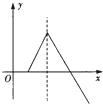 | C、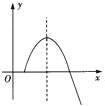 | D、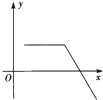 |
分析:根据条件确定点P,对应的轨迹,然后求出相应的周长和面积,求出函数f(x)的表达式,然后根据函数表达式进行判断图象即可.
解答: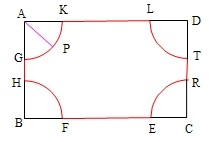 解:∵线段MN的长度为1,线段MN的中点P,
解:∵线段MN的长度为1,线段MN的中点P,
∴AP=
MN=
,
即P的轨迹是分别以A,B,C,D为圆心,半径为
的4个
圆,以及线段GH,FE,RT,LK,部分.
∴G的周长等于四个圆弧长加上线段GH,FE,RT,LK的长,
即周长=2π×
+2(2x-
-
)+2(x-
-
)=π+4x-2+2x-2=6x+π-4,
面积为矩形的面积减去4个
圆的面积,即等于矩形的面积减去一个整圆的面积
为2x•x-π×(
)2=2x2-
,
∴f(x)=6x+π-4-(2x2-
)=-2x2+6x+
-4,是一个开口向下的抛物线,
∴对应的图象为C,
故选:C.
 解:∵线段MN的长度为1,线段MN的中点P,
解:∵线段MN的长度为1,线段MN的中点P,∴AP=
| 1 |
| 2 |
| 1 |
| 2 |
即P的轨迹是分别以A,B,C,D为圆心,半径为
| 1 |
| 2 |
| 1 |
| 4 |
∴G的周长等于四个圆弧长加上线段GH,FE,RT,LK的长,
即周长=2π×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
面积为矩形的面积减去4个
| 1 |
| 4 |
为2x•x-π×(
| 1 |
| 2 |
| π |
| 4 |
∴f(x)=6x+π-4-(2x2-
| π |
| 4 |
| 5π |
| 4 |
∴对应的图象为C,
故选:C.
点评:本题主要考查函数图象的识别和判断,根据条件确定点P的轨迹是解决本题的关键,综合性较强,难度较大.

练习册系列答案
相关题目

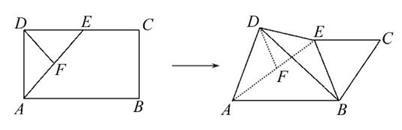
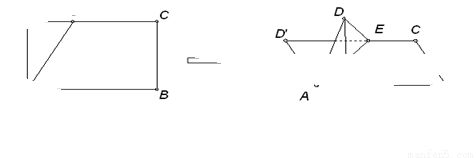
 ,BC=1,E为线段DC上一动点,现将
,BC=1,E为线段DC上一动点,现将 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为
( )
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为
( )
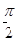 B.
B.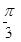 C.
C.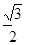 D.
D.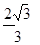
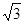 ,BC=1,E为线段DC上一动点,现将
,BC=1,E为线段DC上一动点,现将 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )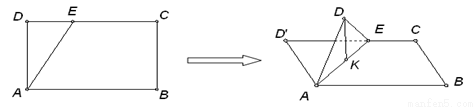
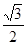 B.
B.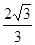 C.
C.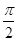 D.
D.