题目内容
为配合即将开幕的2010年上海世博会,某大学拟成立由4名同学组成志愿者招募宣传队,经过初选,2名男同学,4名女同学成为了候选人,每位候选人当选正式队员的机会是相等的.
(1)求当选的4名同学中恰有1名男同学的概率.(2)求当选的4名同学中至少有3名女同学的概率.
(1)求当选的4名同学中恰有1名男同学的概率.(2)求当选的4名同学中至少有3名女同学的概率.
分析:(1)本题是一个等可能事件的概率,试验发生所包含的事件是从6名学生中选出4名,共有C64种结果,满足条件的事件是当选的4名同学中恰有1名男同学,即包括1男3女,共有C43C21种结果,得到概率.
(2)本题是一个等可能事件的概率,所有事件是从6名学生中选出4名,共有C64种结果,满足条件的事件是当选的4名同学中至少有3名女同学,包括两种情况:3女一男;4女,这两种情况是互斥的,共有C43C21+C44,得到概率.
(2)本题是一个等可能事件的概率,所有事件是从6名学生中选出4名,共有C64种结果,满足条件的事件是当选的4名同学中至少有3名女同学,包括两种情况:3女一男;4女,这两种情况是互斥的,共有C43C21+C44,得到概率.
解答:解:(1)由题意知本题是一个等可能事件的概率,
试验发生所包含的事件是从6名学生中选出4名,共有C64=15种结果,
满足条件的事件是当选的4名同学中恰有1名男同学,即包括1男3女,共有C43C21=8种结果
∴当选的4名同学中恰有1名男同学的概率为P(A)=
(2)由题意知本题是一个等可能事件的概率,
试验发生所包含的事件是从6名学生中选出4名,共有C64=15种结果,
满足条件的事件是当选的4名同学中至少有3名女同学,
包括两种情况:3女一男;4女,这两种情况是互斥的,共有C43C21+C44=9种结果,
∴当选的4名同学中至少有3名女同学的概率为P(B)=
试验发生所包含的事件是从6名学生中选出4名,共有C64=15种结果,
满足条件的事件是当选的4名同学中恰有1名男同学,即包括1男3女,共有C43C21=8种结果
∴当选的4名同学中恰有1名男同学的概率为P(A)=
| 8 |
| 15 |
(2)由题意知本题是一个等可能事件的概率,
试验发生所包含的事件是从6名学生中选出4名,共有C64=15种结果,
满足条件的事件是当选的4名同学中至少有3名女同学,
包括两种情况:3女一男;4女,这两种情况是互斥的,共有C43C21+C44=9种结果,
∴当选的4名同学中至少有3名女同学的概率为P(B)=
| 3 |
| 5 |
点评:本题考查等可能事件的概率,本题解题的关键是利用组合数的性质做出事件数,根据等可能事件的概率公式求出概率,本题是一个中档题目.

练习册系列答案
相关题目
为配合新课程的实施,乌鲁木齐市第一中学联合兄弟学校举行了“应用与创新”知识竞赛,共有1500名学生参加了这次竞赛(满分100分,得分全为整数).为了解本次竞赛成绩情况,从中随机抽取了部分学生的竞赛成绩,进行统计,整理见下表:
|
组别 |
分 组 |
频 数 |
频率 |
|
1 |
49.5~59.5 |
60 |
0.12 |
|
2 |
59.5~69.5 |
120 |
0.24 |
|
3 |
69.5~79.5 |
180 |
0.36 |
|
4 |
79.5~89.5 |
130 |
|
|
5 |
89.5~99.5 |
|
0.02 |
|
合 计 |
|
1.00 |
解答下列问题:
(1)在这个问题中,总体是 ,样本是 ,
样本容量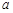 =
;
=
;
(2)第四小组的频率 =
;
=
;
(3)被抽取的学生成绩的中位数落在第几小组内?
(4)若成绩在90分以上(含90分)的学生获一等奖,请你估计此次竞赛获一等奖的人数.
