题目内容
已知定义在区间[-1,1]上的函数 为奇函数..
为奇函数..(1)求实数b的值.
(2)判断函数f(x)在区间(-1,1)上的单调性,并证明你的结论.
(3)f(x)在x∈[m,n]上的值域为[m,n](-1≤m<n≤1 ),求m+n的值.
【答案】分析:(1)依题意,由f(0)=0即可求得b的值;
(2)由(1)得b=0,从而求得f(x)的解析式,利用导数即可判断其增减性;
(3)利用函数的单调性,再结合题意可求得m,n,从而可得到m+n的值.
解答:解:(1)∵定义在区间[-1,1]上的函数f(x)=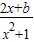 为奇函数,
为奇函数,
∴f(0)=0,即b=0,…(2分)
检验:当b=0时,f(x)=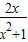 为奇函数,…(3分)
为奇函数,…(3分)
∴b=0.
(2)函数f(x)=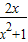 在区间(-1,1)上是增函数…(4分)
在区间(-1,1)上是增函数…(4分)
证明:∵f(x)=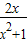 ,
,
∴f′(x)=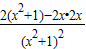
=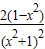 ,…(6分)
,…(6分)
∵x∈(-1,1),
∴f′(x)>0,…(7分)
∴函数f(x)在区间(-1,1)上是增函数 …(8分)
(3)由(2)知函数f(x)在区间[m,n]上是增函数,函数f(x)的值域为[f(m),f(n)]
∴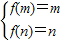 即
即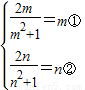 …(9分)
…(9分)
由①得m=-1 或 0或1,
由②得n=-1 或 0或1…(11分)
又∵-1≤m<n≤1
∴m=-1,n=0;或m=-1,n=1;或m=0,n=1…(12)
∴m+n=-1;或m+n=0;或m+n=1…(13)
点评:本题考查利用导数研究函数的单调性,判断出f(x)在(-1,1)上是增函数是解决问题的关键,对m,n的取值情况的讨论是难点,考查综合分析与运算的能力,属于难题.
(2)由(1)得b=0,从而求得f(x)的解析式,利用导数即可判断其增减性;
(3)利用函数的单调性,再结合题意可求得m,n,从而可得到m+n的值.
解答:解:(1)∵定义在区间[-1,1]上的函数f(x)=
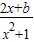 为奇函数,
为奇函数,∴f(0)=0,即b=0,…(2分)
检验:当b=0时,f(x)=
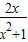 为奇函数,…(3分)
为奇函数,…(3分)∴b=0.
(2)函数f(x)=
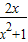 在区间(-1,1)上是增函数…(4分)
在区间(-1,1)上是增函数…(4分)证明:∵f(x)=
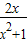 ,
,∴f′(x)=
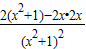
=
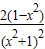 ,…(6分)
,…(6分)∵x∈(-1,1),
∴f′(x)>0,…(7分)
∴函数f(x)在区间(-1,1)上是增函数 …(8分)
(3)由(2)知函数f(x)在区间[m,n]上是增函数,函数f(x)的值域为[f(m),f(n)]
∴
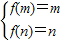 即
即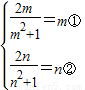 …(9分)
…(9分)由①得m=-1 或 0或1,
由②得n=-1 或 0或1…(11分)
又∵-1≤m<n≤1
∴m=-1,n=0;或m=-1,n=1;或m=0,n=1…(12)
∴m+n=-1;或m+n=0;或m+n=1…(13)
点评:本题考查利用导数研究函数的单调性,判断出f(x)在(-1,1)上是增函数是解决问题的关键,对m,n的取值情况的讨论是难点,考查综合分析与运算的能力,属于难题.

练习册系列答案
相关题目
 为奇函数..
为奇函数.. 为奇函数..
为奇函数..