题目内容
如图,四棱柱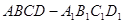 中,
中,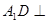 平面
平面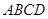 ,底面
,底面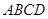 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱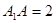 ,
,

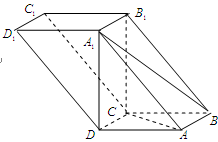
(Ⅰ)证明: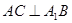 ;
;
(Ⅱ)若棱 上存在一点
上存在一点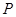 ,使得
,使得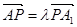 ,
,
当二面角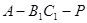 的大小为
的大小为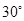 时,求实数
时,求实数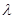 的值.
的值.
【答案】
以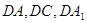 所在直线分别为
所在直线分别为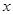 轴,
轴,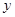 轴,
轴, 轴建系
轴建系
(Ⅱ) .
.
【解析】
试题分析:(I)(Ⅰ)连接BD交AC于点O
∵四边形ABCD是正方形∴AC⊥BD
又∵AD1⊥平面ABCD,AC?平面ABCD
∴AC⊥A1D,A1D∩BD=D∴AC⊥平面A1BD,A1B?平面A1BD
∴AC⊥A1B。
以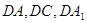 所在直线分别为
所在直线分别为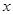 轴,
轴,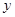 轴,
轴, 轴建系
轴建系
(Ⅱ)∵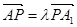 ∴
∴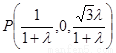 ,设平面
,设平面 的一个法向量为
的一个法向量为 ,
,
 ,
,
令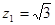 则
则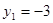 ,
, ,
,
∴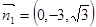 6分
6分
设平面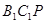 的一个法向量为
的一个法向量为
 ,
,

∴ 8分
8分
 10分
10分
∴ 12分
12分
考点:本题主要考查立体几何中的垂直关系,角的计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用空间向量,省去繁琐的证明,也是解决立体几何问题的一个基本思路。注意运用转化与化归思想,将空间问题转化成平面问题。本题利用空间向量知识解答,关键点是建立适当地空间直角坐标系。

练习册系列答案
相关题目
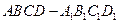 中,
中,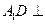 平面
平面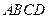 ,底面
,底面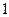 的正方形,侧棱
的正方形,侧棱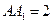 .
.
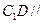 平面
平面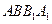 ;
;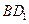 与平面
与平面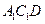 所成角的正弦值.
所成角的正弦值.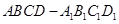 中,
中,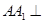 平面
平面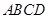 .
.
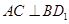 的充分条件,并给予证明;
的充分条件,并给予证明;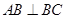 ,②
,②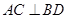 ;③
;③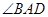 为锐角,求平面
为锐角,求平面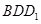 与平面
与平面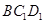 所成锐二面角
所成锐二面角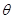 的取值范围.
的取值范围.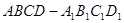 中,
中,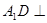 平面
平面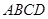 ,底面
,底面 ,
,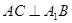 ;
; 上存在一点
上存在一点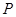 ,使得
,使得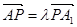 ,
,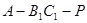 的大小为
的大小为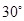 时,求实数
时,求实数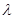 的值.
的值.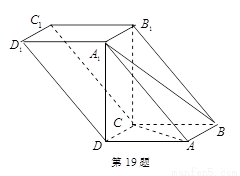
 中,
中, 平面
平面 ,底面
,底面 的正方形,侧棱
的正方形,侧棱 .
.
 平面
平面 ;
; 与平面
与平面