题目内容
小明和同桌小聪一起合作探索:如图,一架5米长的梯子AB斜靠在铅直的墙壁AC上,这时梯子的底端B到墙角C的距离为1.4米.如果梯子的顶端A沿墙壁下滑0.8米,那么底端B将向左移动多少米?

(1)小明的思路如下,请你将小明的解答补充完整:
解:设点B将向左移动x米,即BE=x,则:
EC=
x+1.4,DC=AC-DC= -0.8=4,
-0.8=4,
而DE=5,在Rt△DEC中,由EC2+DC2=DE2,
得方程为: , 解方程得: ,
∴点B将向左移动 米.
(2)解题回顾时,小聪提出了如下两个问题:
①将原题中的“下滑0.8米”改为“下滑1.8米”,那么答案会是1.8米吗?为什么?
②梯子顶端下滑的距离与梯子底端向左移动的距离能相等吗?为什么?
请你解答小聪提出的这两个问题.
(1)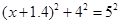 ,
,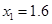
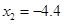 (舍去),1.6
(舍去),1.6
(2)①不会②有可能
【解析】
试题分析:(1)根据题意及勾股定理可知,第一个空应该填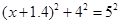 , …1分
, …1分
解方程可得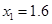 ,
,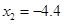 (舍去) …3分
(舍去) …3分
∴点B将向左移动 1.6 米. …4分
(2)①不会是1.8米 …5分
理由:若AD=BE=1.8,则DC=4.8-1.8=3,EC=1.4+1.8=3.2
∵3.22+ 32≠52 ∴该题的答案不会是0.9米. …7分
②有可能 …8分
理由:设梯子顶端从A处下滑a米,点B向左也移动a米,
则有(a+1.4)2+(4.8-a)2=52
解得:a =3.4或a =0(舍去).
∴当梯子顶端从A处下滑3.4米时,点B向左也移动3.4米
即:梯子顶端下滑的距离与梯子底端向左移动的距离有可能相等. …10分
考点:本小题主要考查平面几何在实际问题中的应用,考查学生应用函数知识解决实际问题的能力.
点评:解决实际问题时,要注意实际问题的定义域,还要注意灵活转化,将实际问题转化为熟悉的数学问题解决.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案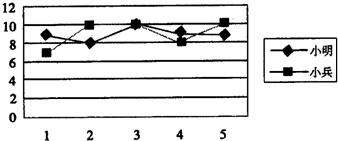 小明和小兵两人参加学校组织的理化实验操作测试,近期的5次测试成绩如图所示,则小明5次成绩的方差S12与小兵5次成绩的方差S22之间的大小关系为S12
小明和小兵两人参加学校组织的理化实验操作测试,近期的5次测试成绩如图所示,则小明5次成绩的方差S12与小兵5次成绩的方差S22之间的大小关系为S12