题目内容
 某开发商对去年市场上一种商品销售数量及销售利润情况进行了调查,发现:
某开发商对去年市场上一种商品销售数量及销售利润情况进行了调查,发现:①销售数量y1(万件)与时间(月份)具有满足如表的一次函数关系:
| 时间x(月份) | 1 | 2 | 3 | … | 11 | 12 |
| 销售数量y1(万件) | 1.7 | 1.8 | 1.9 | … | 2.7 | 2.8 |
请根据以上信息解答下列问题:
(Ⅰ)在三月份,销售这种商品可获利润多少万元?
(Ⅱ)哪一个月的销售利润最大?请说明理由.
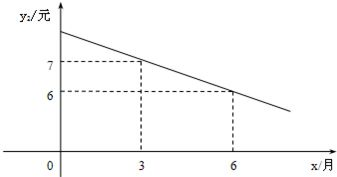
分析:(Ⅰ)由列表知,3月份售出1.9万件,由图象知3月每件销售利润为7元;则利润为7×1.9(万元);
(Ⅱ)由题意,销售数量与月份是一次函数y1=k1x+b1(k1≠0)模型;销售利润与月份是一次函数y2=k2x+b2(k2≠0),月销售利润w=y1y2 整理,得w的最大值.
(Ⅱ)由题意,销售数量与月份是一次函数y1=k1x+b1(k1≠0)模型;销售利润与月份是一次函数y2=k2x+b2(k2≠0),月销售利润w=y1y2 整理,得w的最大值.
解答:解:(Ⅰ)从列表中知道,3月份售出1.9万件;从图象中观察到3月的每件销售利润为7元;
所以,在3月份销售这种商品的利润为:7×1.9=13.3(万元);
(Ⅱ)由题意知,销售数量与月份是一次函数关系,设y1=k1x+b1(k1≠0),则
把x=1时,y1=1.7;x=2时y1=1.8,代入上式得:
解得:k1=0.1,b1=1.6∴y1=0.1x+1.6
由图象知:y2与x是一次函数关系,设y2=k2x+b2(k2≠0),则
把x=3时,y2=7;x=6时,y2=6,代入上式得:
解得:k2=-
,b2=8∴y2=-
x+8;
设月销售利润为w(万元),则:
w=y1y2=(0.1x+1.6)(-
x+8)=-
x2+
x+
=-
(x-4)2+
;
由二次函数的性质知:当x=4时,w的值最大为
(万元).
所以,在3月份销售这种商品的利润为:7×1.9=13.3(万元);
(Ⅱ)由题意知,销售数量与月份是一次函数关系,设y1=k1x+b1(k1≠0),则
把x=1时,y1=1.7;x=2时y1=1.8,代入上式得:
|
解得:k1=0.1,b1=1.6∴y1=0.1x+1.6
由图象知:y2与x是一次函数关系,设y2=k2x+b2(k2≠0),则
把x=3时,y2=7;x=6时,y2=6,代入上式得:
|
解得:k2=-
| 1 |
| 3 |
| 1 |
| 3 |
设月销售利润为w(万元),则:
w=y1y2=(0.1x+1.6)(-
| 1 |
| 3 |
| 1 |
| 30 |
| 4 |
| 15 |
| 64 |
| 5 |
| 1 |
| 30 |
| 40 |
| 3 |
由二次函数的性质知:当x=4时,w的值最大为
| 40 |
| 3 |
点评:本题考查了一次函数,二次函数模型的应用;其中用待定系数法求函数解析式是常用的方法之一.

练习册系列答案
相关题目
某开发商对去年市场上一种商品销售数量及销售利润情况进行了调查,发现:
①销售数量y1(万件)与时间(月份)具有满足如表的一次函数关系:
②每一件______的销售利润y2与时间x(月份)具有如图所示的关系.
请根据以上信息解答下列问题:
(Ⅰ)在三月份,销售这种商品可获利润多少万元?
(Ⅱ)哪一个月的销售利润最大?请说明理由.

①销售数量y1(万件)与时间(月份)具有满足如表的一次函数关系:
| 时间x(月份) | 1 | 2 | 3 | … | 11 | 12 |
| 销售数量y1(万件) | 1.7 | 1.8 | 1.9 | … | 2.7 | 2.8 |
请根据以上信息解答下列问题:
(Ⅰ)在三月份,销售这种商品可获利润多少万元?
(Ⅱ)哪一个月的销售利润最大?请说明理由.

(本小题满分12分)
某开发商对去年市场上一种商品销售数量及销售利润情况进行了调查,发现:
①销售数量y1(万件)与时间(月份)具有满足下表的一次函数关系:
|
时间x(月份) |
1 |
2 |
3 |
… |
11 |
12 |
|
销售数量y1(万件) |
1.7 |
1.8 |
1.9 |
… |
2.7 |
2.8 |
②每一件的销售利润y2与时间x(月份)具有如下图所示的关系。

请根据以上信息解答下列问题:
(Ⅰ)在三月份,销售这种商品可获利润多少万元?
(Ⅱ)哪一个月的销售利润最大?请说明理由。
| 某开发商对去年市场上一种商品销售数量及销售利润情况进行了调查,发现: ①销售数量y1(万件)与时间(月份)具有满足下表的一次函数关系: | ||||||||||||||
| ||||||||||||||
 | ||||||||||||||
| 请根据以上信息解答下列问题: (1)在三月份,销售这种商品可获利润多少万元? (2)哪一个月的销售利润最大?请说明理由, |
(本小题满分12分)
某开发商对去年市场上一种商品销售数量及销售利润情况进行了调查,发现:
①销售数量y1(万件)与时间(月份)具有满足下表的一次函数关系:
| 时间x(月份) | 1 | 2 | 3 | … | 11 | 12 |
| 销售数量y1(万件) | 1.7 | 1.8 | 1.9 | … | 2.7 | 2.8 |
②每一件的销售利润y2与时间x(月份)具有如下图所示的关系。

请根据以上信息解答下列问题:
(Ⅰ)在三月份,销售这种商品可获利润多少万元?
(Ⅱ)哪一个月的销售利润最大?请说明理由。