题目内容
在一个盒子中放有标号分别为1、2、3的三张卡片,现从这个盒子中有放回地先后抽取两张卡片,并记它们的标号分别为x,y,设z=|x-2|+|y-x|,
(1)求事件“z=1”发生的概率;
(2)求z的最大值,并求事件“z取得最大值”的概率.
解:(1)由题意知,本题是一个等可能事件的概率,
试验发生包含的事件是从盒子中有放回地先后抽取两张卡片共包含基本事件9个,
分别为:(1,1),(1,2),(1,3),(2,1),(2,2),
(2,3),(3,1),(3,2),(3,3);
设事件“z=1”为事件A,
满足条件的事件包含的基本事件4个,分别为:(1,1),(2,1),(2,3),(3,3),
∴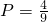 ;
;
(2)由题意知,本题是一个等可能事件的概率,
试验发生包含的事件是从盒子中有放回地先后抽取两张卡片共包含基本事件9个,
分别为:(1,1),(1,2),(1,3),(2,1),(2,2),
(2,3),(3,1),(3,2),(3,3);
z的最大值为3,
设事件“z的最大值”为事件B.
包含基本事件2个,分别为:(1,3),(3,1),
∴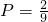 .
.
分析:(1)本题是一个等可能事件的概率,试验发生包含的事件是从盒子中有放回地先后抽取两张卡片列举出来共包含基本事件9个,满足条件的事件根据前面列举出的事件,得到有4个结果,根据概率公式得到概率.
(2)本题是一个等可能事件的概率,试验发生包含的事件是从盒子中有放回地先后抽取两张卡片列举出来共包含基本事件9个,满足条件的事件数可以通过前面的列举得到,根据等可能事件的概率得到结果.
点评:本题考查等可能事件的概率,是概率与绝对值的意义结合的题目,是一个基础题,解题的关键是对于题目中满足条件的事件的理解.
试验发生包含的事件是从盒子中有放回地先后抽取两张卡片共包含基本事件9个,
分别为:(1,1),(1,2),(1,3),(2,1),(2,2),
(2,3),(3,1),(3,2),(3,3);
设事件“z=1”为事件A,
满足条件的事件包含的基本事件4个,分别为:(1,1),(2,1),(2,3),(3,3),
∴
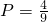 ;
;(2)由题意知,本题是一个等可能事件的概率,
试验发生包含的事件是从盒子中有放回地先后抽取两张卡片共包含基本事件9个,
分别为:(1,1),(1,2),(1,3),(2,1),(2,2),
(2,3),(3,1),(3,2),(3,3);
z的最大值为3,
设事件“z的最大值”为事件B.
包含基本事件2个,分别为:(1,3),(3,1),
∴
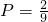 .
.分析:(1)本题是一个等可能事件的概率,试验发生包含的事件是从盒子中有放回地先后抽取两张卡片列举出来共包含基本事件9个,满足条件的事件根据前面列举出的事件,得到有4个结果,根据概率公式得到概率.
(2)本题是一个等可能事件的概率,试验发生包含的事件是从盒子中有放回地先后抽取两张卡片列举出来共包含基本事件9个,满足条件的事件数可以通过前面的列举得到,根据等可能事件的概率得到结果.
点评:本题考查等可能事件的概率,是概率与绝对值的意义结合的题目,是一个基础题,解题的关键是对于题目中满足条件的事件的理解.

练习册系列答案
相关题目
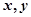 ,设
,设 ,
,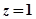 ”发生的概率;
”发生的概率; 的最大值,并求事件“
的最大值,并求事件“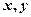 ,设
,设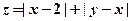 ,
,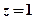 ”发生的概
”发生的概 率;
率; 的最大值,并求事件“
的最大值,并求事件“