题目内容
若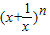 展开式的二项式系数之和为256,则n= ,其展开式的常数项等于 .(用数字作答)
展开式的二项式系数之和为256,则n= ,其展开式的常数项等于 .(用数字作答)
【答案】分析:展开式的二项式系数之和为2n=256,n=8.令展开式中通项x的指数为0,即得常数项.
解答:解:由已知条件可得2n=256,解之得n=8,则二项式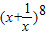 的通项公式为C8rx8-2r,令8-2r=0,得r=4,展开式的常数项为
的通项公式为C8rx8-2r,令8-2r=0,得r=4,展开式的常数项为
C84=70.
故答案为:8 70.
点评:本题考查了二项式系数的性质,二项式定理的简单直接应用.属于基础题.
解答:解:由已知条件可得2n=256,解之得n=8,则二项式
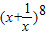 的通项公式为C8rx8-2r,令8-2r=0,得r=4,展开式的常数项为
的通项公式为C8rx8-2r,令8-2r=0,得r=4,展开式的常数项为C84=70.
故答案为:8 70.
点评:本题考查了二项式系数的性质,二项式定理的简单直接应用.属于基础题.

练习册系列答案
相关题目
 展开式的二项式系数和为
展开式的二项式系数和为 ,则展开式中所有理项共有( )项
,则展开式中所有理项共有( )项 展开式的二项式系数之和为64,则展开式的常数项为 。(用数字作答)
展开式的二项式系数之和为64,则展开式的常数项为 。(用数字作答) 展开式的二项式系数之和为64,则展开式的常数项为( )
展开式的二项式系数之和为64,则展开式的常数项为( ) 展开式的二项式系数之和为64,则展开式的常数项为 (
)
展开式的二项式系数之和为64,则展开式的常数项为 (
) 展开式的二项式系数之和为64,则展开式的常数项为( )
展开式的二项式系数之和为64,则展开式的常数项为( )