题目内容
某糖果厂为了拓宽其产品的销售市场,决定对一种半径为1的球形糖果的外层包装进行设计,设计时要求同时满足如下条件:
(1)外包装要呈一封闭的圆锥形状;
(2)为减少包装成本,要求所用材料最省;
(3)为了方便携带,包装后每个糖果的体积最小.问:这些条件能同时满足吗?如果能,如何设计这个圆锥的底面半径和高?此时所用的外包装用料是多少?体积是多少?如不能,请说明理由.
(1)外包装要呈一封闭的圆锥形状;
(2)为减少包装成本,要求所用材料最省;
(3)为了方便携带,包装后每个糖果的体积最小.问:这些条件能同时满足吗?如果能,如何设计这个圆锥的底面半径和高?此时所用的外包装用料是多少?体积是多少?如不能,请说明理由.
分析:假设圆锥母线与底面夹角为2θ,圆锥的全面积=πR(l+R),然后利用二次函数求出其最值,圆锥的体积为V=
Sh,利用二次函数求出最值,看能同时取到最值,从而得到结论.
| 1 |
| 3 |
解答:解:假设圆锥母线与底面夹角为2θ.
圆锥的全面积=πR(l+R)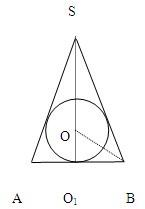
=π•
•
=
.
在圆锥全面积的表达式中,因其分子为常数,所以欲使全面积最小,必须使其分母最大.
tg2θ(1-tg2θ)=
-
(2tg2θ-1)2.
因此,欲使tg2θ(1-tg2θ)最大,必须
2tg2θ-1=0,tgθ=
,(因必为锐,所以仅取正号)
θ=arctg
.
故当θ取值 θ=arctg
时,圆锥的全面积最小.
圆锥的体积为V=
Sh=
π
(1+
)=
×
根据体积的表达式中,因其分子为常数,所以欲使体积最小,必须使其分母最大.
tg2θ(1-tg2θ)=
-
(2tg2θ-1)2.
因此,欲使tg2θ(1-tg2θ)最大,必须
2tg2θ-1=0,tgθ=
,(因必为锐,所以仅取正号)
θ=arctg
.
故当θ取值 θ=arctg
时,圆锥的体积最小.
∴这个圆锥的底面半径为
和高为4,此时所用的外包装用料是8π,体积是
.
圆锥的全面积=πR(l+R)

=π•
| 1 |
| tgθ |
| 2 |
| tgθ(1-tg2θ) |
=
| 2π |
| tg2θ(1-tg2θ) |
在圆锥全面积的表达式中,因其分子为常数,所以欲使全面积最小,必须使其分母最大.
tg2θ(1-tg2θ)=
| 1 |
| 4 |
| 1 |
| 4 |
因此,欲使tg2θ(1-tg2θ)最大,必须
2tg2θ-1=0,tgθ=
| ||
| 2 |
θ=arctg
| ||
| 2 |
故当θ取值 θ=arctg
| ||
| 2 |
圆锥的体积为V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| tg2θ |
| 1 |
| cos2θ |
| π |
| 3 |
| 1 |
| tg2θ |
| 2 |
| 1-tg2θ |
根据体积的表达式中,因其分子为常数,所以欲使体积最小,必须使其分母最大.
tg2θ(1-tg2θ)=
| 1 |
| 4 |
| 1 |
| 4 |
因此,欲使tg2θ(1-tg2θ)最大,必须
2tg2θ-1=0,tgθ=
| ||
| 2 |
θ=arctg
| ||
| 2 |
故当θ取值 θ=arctg
| ||
| 2 |
∴这个圆锥的底面半径为
| 2 |
| 8π |
| 3 |
点评:本题主要考查了函数模型的选择与应用,同时考查了圆锥的体积和表面积,以及最值的求解,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某公司为了了解其产品推销员的工作年限与年推销额之间的关系,收集了公司中的5名产品推销员的推销数据,如下表:
从散点图分析,x与y具有线性相关且回归方程为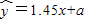 ,则a的值为 .
,则a的值为 .
| 工作年限 x (年) | 1 | 2 | 3 | 4 | 5 |
| 年推销金额y(万元) | 0.5 | 1 | 2 | 3 | 3.5 |
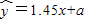 ,则a的值为 .
,则a的值为 . 