题目内容
若曲线y=3x2+bx+c在x=x处切线的倾斜角为45,则点(x,0)到曲线对称轴的距离是( )A.

B.

C.

D.
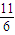
【答案】分析:先根据切线的倾斜角求出斜率,而切线的斜率就是曲线在切点处的导数,据此求出曲线在点(x,0)处的导数,找到x和b的关系,用b表示x,再带着参数b求出点(x,0)到曲线对称轴的距离,消去参数,可得结果.
解答:解:∵曲线y=3x2+bx+c在x=x处切线的倾斜角为45,∴切线的斜率等于1,
∴曲线y=3x2+bx+c在x=x处的导数等于1,
对曲线y=3x2+bx+c求导,得,y′=6x+b,
∴6x+b=1,x=
∵曲线y=3x2+bx+c对称轴为x=-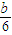 ,
,
∴(x,0)到对称轴的距离为|x+ |=|
|=|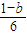 +
+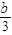 |=
|=
故选A
点评:本题主要考查直线倾斜角与斜率关系,曲线的切线斜率与切点处的导数的关系,以及点到直线的距离的求法.属于综合题.
解答:解:∵曲线y=3x2+bx+c在x=x处切线的倾斜角为45,∴切线的斜率等于1,
∴曲线y=3x2+bx+c在x=x处的导数等于1,
对曲线y=3x2+bx+c求导,得,y′=6x+b,
∴6x+b=1,x=

∵曲线y=3x2+bx+c对称轴为x=-
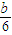 ,
,∴(x,0)到对称轴的距离为|x+
 |=|
|=|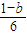 +
+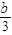 |=
|=
故选A
点评:本题主要考查直线倾斜角与斜率关系,曲线的切线斜率与切点处的导数的关系,以及点到直线的距离的求法.属于综合题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目



