题目内容
将一颗六个面上分别标有1,2,3,4,5,6的骰子先后抛掷2次,观察向上的点数,则“点数之和是3的倍数”的概率是 .
【答案】分析:本题是一个古典概型,试验发生包含的事件是一颗骰子抛掷2次向上的点数,共有36种结果,满足条件的事件是点数之和是3的倍数,可以列举出结果,根据古典概型概率公式得到结果.
解答:解:由题意知本题是一个古典概型,
试验发生包含的事件是一颗骰子抛掷2次,观察向上的点数,共有36种结果,
满足条件的事件是点数之和是3的倍数,可以列举出有12种结果,
根据古典概型概率公式得到P=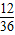 =
= ,
,
故答案为:
点评:本题考查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,应用列举法来解题是这一部分的最主要思想.
解答:解:由题意知本题是一个古典概型,
试验发生包含的事件是一颗骰子抛掷2次,观察向上的点数,共有36种结果,
满足条件的事件是点数之和是3的倍数,可以列举出有12种结果,
根据古典概型概率公式得到P=
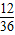 =
= ,
,故答案为:

点评:本题考查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,应用列举法来解题是这一部分的最主要思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目