题目内容
如图所示,在圆心角为直角的扇形OAB中,分别以OA、OB为直径作两个半圆,在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )

(A) -
-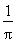 (B)
(B)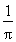
(C)1- (D)
(D)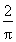
【答案】
C
【解析】如图,不妨设扇形的半径为2a,如图,记两块白色区域的面积分别为S1,S2,两块阴影部分的面积分别为S3,S4,

则S1+S2+S3+S4= =
= π(2a)2=πa2①
π(2a)2=πa2①
而S1+S3与S2+S3的和恰好为一个半径为a的圆的面积,
即S1+S3+S2+S3=πa2.②
①-②得S3=S4,
由图可知S3=(S扇形EOD+S扇形COD)-S正方形OEDC=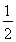 πa2-a2,
πa2-a2,
所以S阴影=πa2-2a2.
由几何概型概率公式可得,此点取自阴影部分的概率为
p= =
= =1-
=1-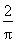 .故选C.
.故选C.

练习册系列答案
相关题目
 如图所示,在半径为
如图所示,在半径为

 ,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上.设矩形PNMQ的面积为y,∠POB=θ,将y表示成θ的函数关系式,并求出y的最大值.
,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上.设矩形PNMQ的面积为y,∠POB=θ,将y表示成θ的函数关系式,并求出y的最大值.