题目内容
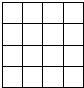
10、将红、黑、白三个棋子放入如图所示的小方格内，每格只能放一个棋子，且3个棋子既不同行也不同列，则不同的放法有（ ）
分析：由题意知本题用分步计数原理，先从16个格子中任选一格放一个棋子，3个棋子既不同行也不同列，剩下的只有9个格子可以放，只有4个格子可以放，根据分步计数原理得到结果．
解答：解：由题意知本题用分步计数原理，
第一步先从16个格子中任选一格放一个棋子有16中方法，
第二步3个棋子既不同行也不同列，剩下的只有9个格子可以放有9种方法，
第三步只有4个格子可以放，有4种方法，
由 分步计数原理知共有16×9×4=576，
故选A．
第一步先从16个格子中任选一格放一个棋子有16中方法，
第二步3个棋子既不同行也不同列，剩下的只有9个格子可以放有9种方法，
第三步只有4个格子可以放，有4种方法，
由 分步计数原理知共有16×9×4=576，
故选A．
点评：本题应用计数原理解决，必须且只需连续完成这3个步骤，这件事才算完成．用两个计数原理解决计数问题时，最重要的是在开始计算之前要进行仔细分析要完成的“一件事”是什么，可以“分类”还是需要“分步”．
练习册系列答案
相关题目
个棋子既不同行也不同列，则不同的放法有（ ）
种 B. 
种 C. 
种 D. 
种
