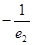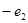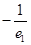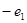题目内容
等比数列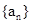 中,
中,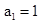 ,公比q=2,则数列
,公比q=2,则数列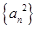 的前4项和为
的前4项和为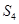 =( )
=( )
| A.85 | B.225 | C.15 | D.7225 |
A
解析试题分析:∵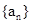 是等比数列
是等比数列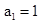 ,公比
,公比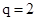 ,
,
∴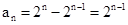 ,
,
∴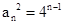 是等比数列,
是等比数列,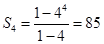 ,故选A.
,故选A.
考点:等比数列的通项公式、求和公式.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
已知数列 的前
的前 项的和
项的和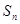 满足
满足 ,则数列
,则数列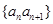 的前
的前 项的和为( )
项的和为( )
A.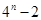 | B.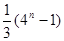 | C.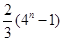 | D.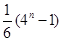 |
在等比数列 中,
中,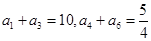 ,则公比
,则公比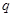 等于( )
等于( )
| A.2 | B. | C.-2 | D.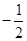 |
设 若
若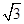 是
是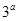 与
与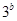 的等比中项,则
的等比中项,则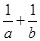 的最小值为( )
的最小值为( )
| A.8 | B.4 | C.1 | D.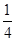 |
在正项等比数列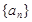 中,
中,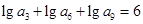 ,则
,则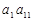 的值是( )
的值是( )
A.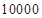 | B.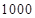 | C.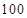 | D.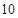 |
在各项都为正数的等比数列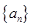 中,
中,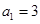 ,前三项的和为
,前三项的和为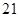 ,则
,则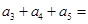 ( )
( )
A.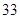 | B.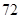 | C. | D.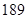 |
已知数列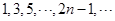 则
则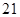 是这个数列的
是这个数列的
| A.第10项 | B.第11项 | C.第12项 | D.第21项 |
设等比数列{an}的公比q=2,前n项和为Sn,若S4=1,则S8= ( ).
| A.17 | B.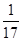 | C.5 | D.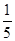 |
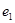 的椭圆与离心率为
的椭圆与离心率为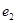 的双曲线有相同的焦点,且椭圆长轴的端点、短轴的端点、焦点到双曲线的一条渐近线的距离依次构成等比数列,则
的双曲线有相同的焦点,且椭圆长轴的端点、短轴的端点、焦点到双曲线的一条渐近线的距离依次构成等比数列,则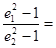 ( )
( )