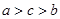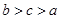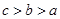题目内容
已知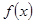 是R上的偶函数,且在区间
是R上的偶函数,且在区间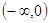 上是增函数,若
上是增函数,若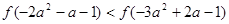 ,那么实数
,那么实数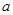 的取值范围是( )
的取值范围是( )
| A.(-1,0) | B.(-∞,0)∪(3,+∞) | C.(3,+∞) | D.(0,3) |
D
解析考点:奇偶性与单调性的综合;抽象函数及其应用.
分析:利用函数的单调性,将函数值的大小关系转化为自变量的关系得出关于a的不等式是解决本题的关键,还要注意整体自变量的取值是否属于该定义区间.
解:由于-2a2-a-1=-2((a+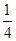 )2+
)2+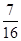 )<0,-3a2+2a-1=-3((a-
)<0,-3a2+2a-1=-3((a-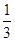 )2+
)2+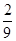 )<0,
)<0,
故-2a2-a-1,-3a2+2a-1均在区间(-∞,0)上,
因此f(-2a2-a-1)<f(-3a2+2a-1)?-2a2-a-1<-3a2+2a-1,
解得a∈(0,3).
故选D.

练习册系列答案
相关题目
若关于x的方程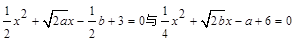 在R上都有解,则
在R上都有解,则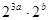 的最小值为:( )
的最小值为:( )
| A.256 | B. 128 | C. 64 | D.32 |
已知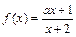 在
在 上是增函数,则
上是增函数,则 的取值范围是
的取值范围是
A. | B. 或 或 | C. | D. |
下列四组函数,表示同一函数的是
A.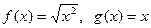  | B.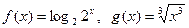 |
C.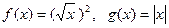 | D.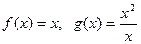 |
甲乙两人同时驾车从A地出发前往B地,他们都曾经以速度 或
或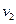 行驶,在全程中,甲的时间速度关系如图甲,乙的路程速度关系如图乙,那么下列说法正确的是
行驶,在全程中,甲的时间速度关系如图甲,乙的路程速度关系如图乙,那么下列说法正确的是
A.甲先到达B地  | B.乙先到达B地 |
C.甲乙同时到 达B地 达B地 | D.无法确定谁先到达B地 |
下列四个函数中,在区间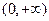 上单调递增的函数是 ( )
上单调递增的函数是 ( )
A.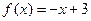 | B.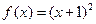 | C.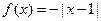 | D.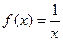 |
函数y=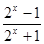 是( )
是( )
| A.奇函数 | B.偶函数 | C.非奇非偶函数 | D.既是奇函数又是偶函数 |
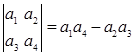 ,将函数
,将函数 的图像向左平移
的图像向左平移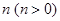 个单位,所得图像对应的函数为偶函数,则
个单位,所得图像对应的函数为偶函数,则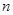 的最小值为 ( )
的最小值为 ( )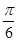
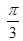
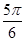
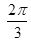
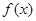 满足
满足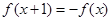 ,且在[-1,0]上单调递增,
,且在[-1,0]上单调递增,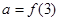 ,
,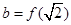 ,
,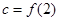 ,则
,则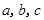 的大小关系是( )
的大小关系是( )