Question

（本题总分14分）已知函数＝ax²+x-3,g(x)=-x+4lnx

h(x)=-g(x)

(1)当a=1时，求函数h(x)的极值。

（2）若函数h(x)有两个极值点，求实数a的取值范围。

（3）定义：对于函数F（x）和G（x），若存在直线l:y=kx+b，使得对于函数F（x）和

G（x）各自定义域内的任意x，都有F（x）≥kx+b且G（x）≤kx+b成立，则称直线l:y=kx+b为函数F（x）和G（x）的“隔离直线”。则当a=1时，函数和g(x)是否存在“隔离直线”。若存在，求出所有的“隔离直线”。若不存在，请说明理由。

Answer 1

解：（1）a=1时，＝，，

的定义域是（0，+∞），

当x∈(0,1)时，递减

当x∈(1，+∞)时，递增

∴x=1时，h(x)取得极小值h(1)=0,h(x)无极大值。…………（4分）

（2），x∈(0,+∞)

依题意，方程在（0，+∞）上有两个不相等的解。

∴∴-

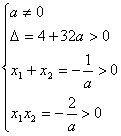∴a的取值范围是（-）…………………………（9分）

（3）设存在，a=1时，

由（1）知，当且仅当x＝1时，h(x)=0,此时，f(1)=g(1)=-1

∴y=与y=g(x)的图象有唯一的交点A（1，-1）

直线l必过点A，设l的方程：y+1=k(x-1),y=kx-k-1

由≥kx-k-1恒成立得x²+(1-k)x+k-2≥0恒成立

∴△＝（1-k）²-4(k-2)=(k-3)²≤0

∴k=3,直线l的方程：y=3x-4………………………………（12分）

以下证明g(x)≤3x-4对x>0恒成立

令φ（x）＝3x-4-g(x)=4x-4-4lnx

φ`(x)=4-

当x∈(0,1)时 , φ`(x)<0, φ(x)递减，当x∈（1，+∞）时，φ(x)>0，φ(x)递增，∴φ(x)的最小值为φ(1)＝0，∴φ(x)≥0恒成立

即g(x)≤3x-4对x>0恒成立

综上，和g(x)存在唯一的“隔离直线”：y=3x-4。……（14分）