题目内容
右图是一个容量为200的样本的频率分布直方图，请根据图形中的数据填空：
（1）样本数据落在范围
的频率为
；
（2）样本数据落在范围
的频数为
；
答案：0.32 72
解析：
解析：
解：(1) 样本数据落在范围
|
的频率为0.08×4=0.32，(2) 样本数据落在范围
的频数为200×0.36=72.
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
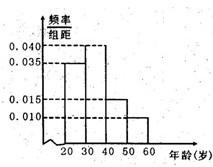某工厂有120名工人，其年龄都在20～60岁之间，各年龄段人数按[20，30），[30，40），[40，50），[50，60]分组，其频率分布直方图如右图所示，工厂为了开发新产品，引进了新的生产设备，要求每个工人都要参加A、B两项培训，培训结束后进行结业考试，已知各年龄段两项培训结业考试成绩优秀的人数如下表所示，假设两项培训是相互独立的，结业考试也互不影响．| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20，30） | 30 | 18 |
| [30，40） | 36 | 24 |
| [40，50） | 12 | 9 |
| [50，60] | 4 | 3 |
（2）随机从年龄段[20，30）和[30，40）中各抽取1人，设这两人中A、B两项培训结业考试成绩都优秀的人数为X，求X的分布列和数学期望．
《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20～80mg/100ml（不含80）之间，属于酒后驾车；在80mg/100ml（含80）以上时，属醉酒驾车，对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚．
据《法制晚报》报道，2010年8月1日至8月28日，某市交管部门共抽查了1000辆车，查出酒后驾车和醉酒驾车的驾驶员80人，右图是对这80人血液中酒精含量进行检测所得结果的频率分布直方图．
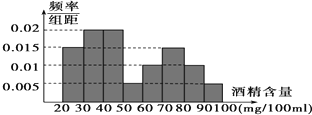
（Ⅰ）根据频率分布直方图完成下表：
（Ⅱ）根据上述数据，求此次抽查的1000人中属于醉酒驾车的概率；
（Ⅲ）若用分层抽样的方法从血液酒精浓度在[70，90）范围内的驾驶员中抽取一个容量为5的样本，并将该样本看成一个总体，从中任取2人，求恰有1人属于醉酒驾车的概率．
据《法制晚报》报道，2010年8月1日至8月28日，某市交管部门共抽查了1000辆车，查出酒后驾车和醉酒驾车的驾驶员80人，右图是对这80人血液中酒精含量进行检测所得结果的频率分布直方图．
（Ⅰ）根据频率分布直方图完成下表：
| 酒精含量 （单位：mg/100ml） |
[20，30） | [30，40） | [40，50） | [50，60） | [60，70） | [70，80） | [80，90） | [90，100） |
| 人数 |
（Ⅲ）若用分层抽样的方法从血液酒精浓度在[70，90）范围内的驾驶员中抽取一个容量为5的样本，并将该样本看成一个总体，从中任取2人，求恰有1人属于醉酒驾车的概率．
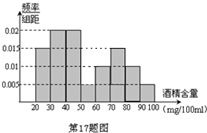《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20～80mg/100ml（不含80）之间，属于酒后驾车；在80mg/100ml（含80）以上时，属醉酒驾车，对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚．
据《法制晚报》报道，2010年8月1日至8月28日，某市交管部门共抽查了1000辆车，查出酒后驾车和醉酒驾车的驾驶员80人，右图是对这80人血液中酒精含量进行检测所得结果的频率分布直方图．
（Ⅰ）根据频率分布直方图完成下表：
| 酒精含量 （单位：mg/100ml） | [20，30） | [30，40） | [40，50） | [50，60） | [60，70） | [70，80） | [80，90） | [90，100） |
| 人数 |
（Ⅲ）若用分层抽样的方法从血液酒精浓度在[70，90）范围内的驾驶员中抽取一个容量为5的样本，并将该样本看成一个总体，从中任取2人，求恰有1人属于醉酒驾车的概率．
《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20～80mg/100ml（不含80）之间，属于酒后驾车；在80mg/100ml（含80）以上时，属醉酒驾车，对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚．
据《法制晚报》报道，2010年8月1日至8月28日，某市交管部门共抽查了1000辆车，查出酒后驾车和醉酒驾车的驾驶员80人，右图是对这80人血液中酒精含量进行检测所得结果的频率分布直方图．
（Ⅰ）根据频率分布直方图完成下表：
（Ⅱ）根据上述数据，求此次抽查的1000人中属于醉酒驾车的概率；
（Ⅲ）若用分层抽样的方法从血液酒精浓度在[70，90）范围内的驾驶员中抽取一个容量为5的样本，并将该样本看成一个总体，从中任取2人，求恰有1人属于醉酒驾车的概率．
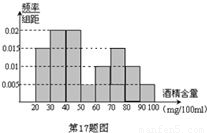
据《法制晚报》报道，2010年8月1日至8月28日，某市交管部门共抽查了1000辆车，查出酒后驾车和醉酒驾车的驾驶员80人，右图是对这80人血液中酒精含量进行检测所得结果的频率分布直方图．
（Ⅰ）根据频率分布直方图完成下表：
| 酒精含量 （单位：mg/100ml） | [20，30） | [30，40） | [40，50） | [50，60） | [60，70） | [70，80） | [80，90） | [90，100） |
| 人数 |
（Ⅲ）若用分层抽样的方法从血液酒精浓度在[70，90）范围内的驾驶员中抽取一个容量为5的样本，并将该样本看成一个总体，从中任取2人，求恰有1人属于醉酒驾车的概率．
某工厂有120名工人，其年龄都在20～60岁之间，各年龄段人数按[20，30），[30，40），[40，50），[50，60]分组，其频率分布直方图如右图所示，工厂为了开发新产品，引进了新的生产设备，要求每个工人都要参加A、B两项培训，培训结束后进行结业考试，已知各年龄段两项培训结业考试成绩优秀的人数如下表所示，假设两项培训是相互独立的，结业考试也互不影响．
（1）若用分层抽样法从全厂工人中抽取一个容量为40的样本，求各年龄段应分别抽取的人数，并估计全厂工人的平均年龄；
（2）随机从年龄段[20，30）和[30，40）中各抽取1人，设这两人中A、B两项培训结业考试成绩都优秀的人数为X，求X的分布列和数学期望．
| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20，30） | 30 | 18 |
| [30，40） | 36 | 24 |
| [40，50） | 12 | 9 |
| [50，60] | 4 | 3 |
（2）随机从年龄段[20，30）和[30，40）中各抽取1人，设这两人中A、B两项培训结业考试成绩都优秀的人数为X，求X的分布列和数学期望．