题目内容
一只蚂蚁在边长分别为5,6,| 13 |
分析:先画示意图,在△ABC中利用用余弦定理得三角形的内角B的余弦值进而求得三角形的面积,再求出图中阴影部分的面积,最后利用几何概型即可救是本题中蚂蚁恰在离三个顶点距离都大于1的地方的概率.
解答: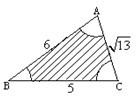 解:画示意图,在△ABC中用余弦定理得cosB=
解:画示意图,在△ABC中用余弦定理得cosB=
,
则sinB=
,S△ABC=
•5•6•
=9,
图中阴影部分的面积为三角形ABC的面积减去半径为1的半圆的面积即为9-
,
则本题中蚂蚁恰在离三个顶点距离都大于1的地方的概率为P=
=1-
.
故答案为:1-
.
 解:画示意图,在△ABC中用余弦定理得cosB=
解:画示意图,在△ABC中用余弦定理得cosB=| 4 |
| 5 |
则sinB=
| 3 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
图中阴影部分的面积为三角形ABC的面积减去半径为1的半圆的面积即为9-
| π |
| 2 |
则本题中蚂蚁恰在离三个顶点距离都大于1的地方的概率为P=
9-
| ||
| 9 |
| π |
| 18 |
故答案为:1-
| π |
| 18 |
点评:本题主要考查了余弦定理、几何概型的应用;简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.

练习册系列答案
相关题目
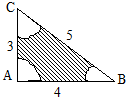 如图,一只蚂蚁在边长分别为3,4,5的三角形区域内随机爬行,则其恰在离三个顶点距离都大于1的地方的概率为( )
如图,一只蚂蚁在边长分别为3,4,5的三角形区域内随机爬行,则其恰在离三个顶点距离都大于1的地方的概率为( )A、
| ||
B、1-
| ||
C、1-
| ||
D、1-
|

 B.
B. C.
C. D.
D.