题目内容

已知数列an共10项，其中an=
1
3n
，则前k项和大于
13
27
的概率是
 
．
分析：根据等比数列的性质先求出数列an的前n项和的表达式，然后即可求出前k项和大于
13
27
的概率．
解答：解：有数列an的通项公式可知：前k项的和Sk=
1
2
（1-
1
3
k）
当Sk≤
13
27
时，即
1
2
（1-
1
3
k）≤
13
27
，解得k≤3，
∴当要想使前k项和大于
13
27
，k必须大于3，
∵数列an共10项，即k有7种取值，
故前k项和大于
13
27
的概率是
7
10
，
故答案为
7
10
．
点评：本题主要考查了等比数列的前n项和的求法以及几何概型，考查了学生的计算能力和对知识的综合掌握，属于基础题．
练习册系列答案
相关题目
已知一列非零向量
an
，n∈N*，满足：
a1
=（10，-5），
an
=(xn，yn)=k(xn-1-yn-1，xn-1+yn-1)，（n32 ）．，其中k是非零常数．
（1）求数列{|
an
|}是的通项公式；
（2）求向量
an-1
与
an
的夹角；（n≥2）；
（3）当k=
1
2
时，把
a1
，
a2
，…，
an
，…中所有与
a1
共线的向量按原来的顺序排成一列，记为
b1
，
b2
，…，
bn
，…，令
OBn
=
b1
+
b2
+…+
bn
，O为坐标原点，求点列{Bn}的极限点B的坐标．（注：若点坐标为（tn，sn），且
lim
n→∞
tn=t，
lim
n→∞
sn=s，则称点B（t，s）为点列的极限点．）
已知一列非零向量
an
，n∈N*，满足：
a1
=（10，-5），
an
=(xn，yn)=k(xn-1-yn-1，xn-1+yn-1)，（n32 ）．，其中k是非零常数．
（1）求数列{|
an
|}是的通项公式；
（2）求向量
an-1
与
an
的夹角；（n≥2）；
（3）当k=
1
2
时，把
a1
，
a2
，…，
an
，…中所有与
a1
共线的向量按原来的顺序排成一列，记为
b1
，
b2
，…，
bn
，…，令
OBn
=
b1
+
b2
+…+
bn
，O为坐标原点，求点列{Bn}的极限点B的坐标．（注：若点坐标为（tn，sn），且
lim
n→∞
tn=t，
lim
n→∞
sn=s，则称点B（t，s）为点列的极限点．）
已知数列an共10项，其中an=
1
3n
，则前k项和大于
13
27
的概率是______．
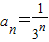已知数列an共10项，其中，则前k项和大于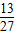的概率是    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网