题目内容
如图,已知△AOB,∠AOB=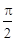 ,∠BAO=
,∠BAO=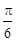 ,AB=4,D为线段AB的中点.若△AOC是△AOB绕直线AO旋转而成的.记二面角B-AO-C的大小为
,AB=4,D为线段AB的中点.若△AOC是△AOB绕直线AO旋转而成的.记二面角B-AO-C的大小为 .
.
(Ⅰ)当平面COD⊥平面AOB时,求 的值;
的值;
(Ⅱ)当 ∈[
∈[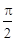 ,
,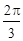 ]时,求二面角C-OD-B的余弦值的取值范围.
]时,求二面角C-OD-B的余弦值的取值范围.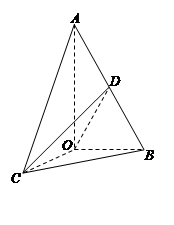
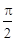 ,∠BAO=
,∠BAO=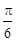 ,AB=4,D为线段AB的中点.若△AOC是△AOB绕直线AO旋转而成的.记二面角B-AO-C的大小为
,AB=4,D为线段AB的中点.若△AOC是△AOB绕直线AO旋转而成的.记二面角B-AO-C的大小为 .
.(Ⅰ)当平面COD⊥平面AOB时,求
 的值;
的值;(Ⅱ)当
 ∈[
∈[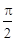 ,
,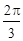 ]时,求二面角C-OD-B的余弦值的取值范围.
]时,求二面角C-OD-B的余弦值的取值范围.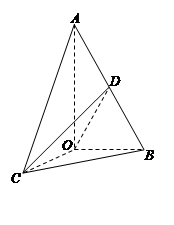
(Ⅰ)如图,以O为原点,在平面OBC内垂直于OB的直线为x轴,OB,OA所在的直线分别为y轴,z轴建立空间直角坐标系O-xyz,则A (0,0,2 ),B (0,2,0), D (0,1,
),B (0,2,0), D (0,1, ),C (2sin
),C (2sin ,2cos
,2cos ,0).设
,0).设 =(x,y,z)为平面COD的一个法向量,
=(x,y,z)为平面COD的一个法向量,
由 得
得 ,
,
取z=sin ,则
,则 =(
=( cos
cos ,-
,- sin
sin ,sin
,sin ).
).
因为平面AOB的一个法向量为 =(1,0,0),
=(1,0,0),
由平面COD⊥平面AOB得

 =0,
=0,
所以cos =0,即
=0,即 =
=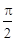 . ………………7分
. ………………7分

(Ⅱ)设二面角C-OD-B的大小为 ,由(Ⅰ)得当
,由(Ⅰ)得当 =
=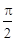 时, cos
时, cos =0;
=0;
当 ∈(
∈(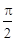 ,
,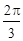 ]时,tan
]时,tan ≤-
≤- ,
,
cos =
=  =
= =-
=- , 故-
, 故- ≤cos
≤cos <0.
<0.
综上,二面角C-OD-B的余弦值的取值范围为[- ,0].
,0].
 ),B (0,2,0), D (0,1,
),B (0,2,0), D (0,1, ),C (2sin
),C (2sin ,2cos
,2cos ,0).设
,0).设 =(x,y,z)为平面COD的一个法向量,
=(x,y,z)为平面COD的一个法向量, 由
 得
得 ,
,取z=sin
 ,则
,则 =(
=( cos
cos ,-
,- sin
sin ,sin
,sin ).
).因为平面AOB的一个法向量为
 =(1,0,0),
=(1,0,0),由平面COD⊥平面AOB得


 =0,
=0,所以cos
 =0,即
=0,即 =
=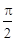 . ………………7分
. ………………7分
(Ⅱ)设二面角C-OD-B的大小为
 ,由(Ⅰ)得当
,由(Ⅰ)得当 =
=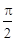 时, cos
时, cos =0;
=0;当
 ∈(
∈(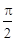 ,
,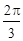 ]时,tan
]时,tan ≤-
≤- ,
,cos
 =
=  =
= =-
=- , 故-
, 故- ≤cos
≤cos <0.
<0.综上,二面角C-OD-B的余弦值的取值范围为[-
 ,0].
,0].(1)平面COD⊥平面AOB,建立坐标系,根据法向量互相垂直求得;(Ⅱ)求两个平面的法向量的夹角。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
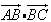 = 1则
= 1则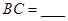




 ,且
,且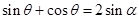 ,
, ,
,
 m
m m
m m
m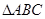 中,
中,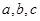 分别是角
分别是角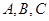 的对边,
的对边,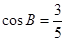 且
且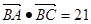
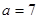 ,求角
,求角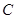 。
。 的三个内角
的三个内角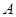 、
、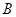 、
、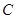 所对的边分别为
所对的边分别为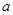 、
、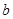 、
、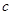 ,向
,向 量
量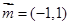 ,
,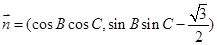 ,且
,且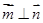 .
.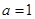 ,
,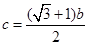 ,求
,求 ,
,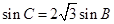 ,求A
,求A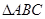 中,a,b,c分别是角A,B,C的对边,向量
中,a,b,c分别是角A,B,C的对边,向量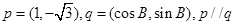 且
且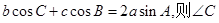 =( )
=( )



 ,b=
,b= ,B=120o,则a等于 ( )
,B=120o,则a等于 ( ) 

