题目内容
计算:(1)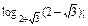
(2)2(lg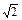 )2+lg
)2+lg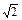 ·lg5+
·lg5+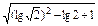 ;
;
(3)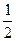 lg
lg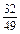 -
-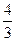 lg
lg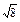 +lg
+lg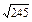 .
.
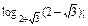
(2)2(lg
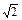 )2+lg
)2+lg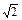 ·lg5+
·lg5+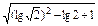 ;
;(3)
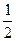 lg
lg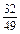 -
-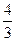 lg
lg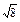 +lg
+lg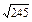 .
.(1)-1(2)1(3)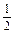
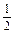
(1)方法一 利用对数定义求值
设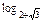 (2-
(2-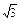 )=x,则(2+
)=x,则(2+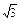 )x=2-
)x=2-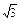 =
=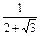 =(2+
=(2+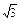 )-1,∴x=-1.
)-1,∴x=-1.
方法二 利用对数的运算性质求解
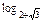 (2-
(2-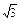 )=
)=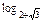
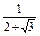 =
=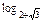 (2+
(2+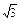 )-1=-1.
)-1=-1.
(2)原式=lg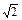 (2lg
(2lg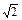 +lg5)+
+lg5)+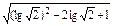 =lg
=lg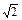 (lg2+lg5)+|lg
(lg2+lg5)+|lg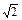 -1|
-1|
=lg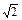 +(1-lg
+(1-lg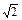 )=1.
)=1.
(3)原式=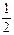 (lg32-lg49)-
(lg32-lg49)-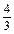 lg8
lg8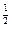 +
+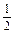 lg245
lg245
=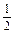 (5lg2-2lg7)-
(5lg2-2lg7)-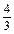 ×
×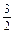 lg2+
lg2+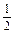 (2lg7+lg5)
(2lg7+lg5)
=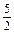 lg2-lg7-2lg2+lg7+
lg2-lg7-2lg2+lg7+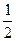 lg5=
lg5=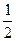 lg2+
lg2+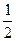 lg5
lg5
=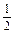 lg(2×5)=
lg(2×5)= 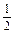 lg10=
lg10=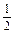 .
.
设
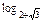 (2-
(2-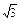 )=x,则(2+
)=x,则(2+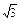 )x=2-
)x=2-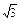 =
=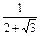 =(2+
=(2+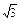 )-1,∴x=-1.
)-1,∴x=-1.方法二 利用对数的运算性质求解
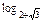 (2-
(2-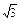 )=
)=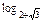
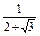 =
=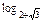 (2+
(2+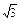 )-1=-1.
)-1=-1.(2)原式=lg
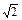 (2lg
(2lg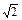 +lg5)+
+lg5)+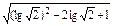 =lg
=lg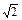 (lg2+lg5)+|lg
(lg2+lg5)+|lg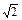 -1|
-1|=lg
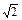 +(1-lg
+(1-lg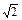 )=1.
)=1.(3)原式=
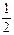 (lg32-lg49)-
(lg32-lg49)-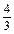 lg8
lg8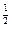 +
+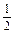 lg245
lg245=
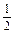 (5lg2-2lg7)-
(5lg2-2lg7)-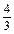 ×
×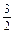 lg2+
lg2+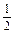 (2lg7+lg5)
(2lg7+lg5)=
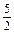 lg2-lg7-2lg2+lg7+
lg2-lg7-2lg2+lg7+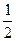 lg5=
lg5=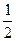 lg2+
lg2+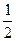 lg5
lg5=
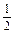 lg(2×5)=
lg(2×5)= 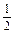 lg10=
lg10=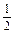 .
.
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 ,
, ,试比较
,试比较 与
与 的大小。
的大小。 、
、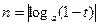 ,则
,则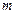 与
与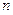 的大小关系为______.
的大小关系为______.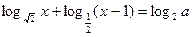 有解,则实数a的取值范围是
有解,则实数a的取值范围是  ,求证:
,求证: 或
或 .
.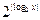 的图象大致是( )
的图象大致是( )