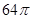题目内容
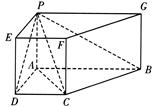
在三棱拄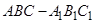 中,
中,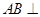 侧面
侧面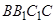 ,已知
,已知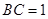 ,
,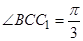 ,
,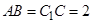 .
.
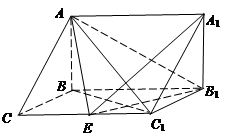
(Ⅰ)求证: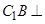 平面
平面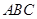 ;
;
(Ⅱ)试在棱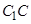 (不包含端点
(不包含端点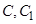 )上确定一点
)上确定一点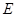 的位置,使得
的位置,使得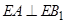 ;
;
(Ⅲ)在(Ⅱ)的条件下,求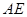 和平面
和平面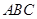 所成角正弦值的大小.
所成角正弦值的大小.
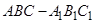 中,
中,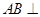 侧面
侧面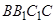 ,已知
,已知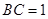 ,
,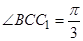 ,
,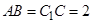 .
.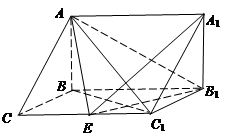
(Ⅰ)求证:
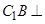 平面
平面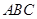 ;
;(Ⅱ)试在棱
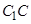 (不包含端点
(不包含端点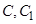 )上确定一点
)上确定一点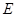 的位置,使得
的位置,使得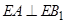 ;
;(Ⅲ)在(Ⅱ)的条件下,求
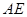 和平面
和平面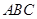 所成角正弦值的大小.
所成角正弦值的大小. (Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)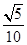
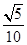
试题分析:(Ⅰ)欲证线面垂直,先考察线线垂直,易证
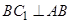 ,可试证
,可试证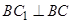 ,由题目给条件易想到利用勾股定理逆定理;(Ⅱ)要想在棱
,由题目给条件易想到利用勾股定理逆定理;(Ⅱ)要想在棱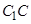 找到点
找到点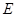 ,使得
,使得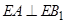 ,易知
,易知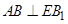 ,那么这时就需要使
,那么这时就需要使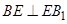 ,这时就转化为一个平面几何问题:以矩形
,这时就转化为一个平面几何问题:以矩形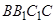 的边
的边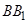 为直径作圆,与
为直径作圆,与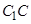 的公共点即为所求,易知只有一点即
的公共点即为所求,易知只有一点即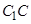 的中点 ,将以上分析写成综合法即可,找到这一点后,也可用别的方法证明,如勾股定理逆定理;(Ⅲ)求直线与平面所成的角,根据其定义,应作出这条直线在平面中的射影,再求这条直线与其射影的夹角(三角函数值),本题可考虑点
的中点 ,将以上分析写成综合法即可,找到这一点后,也可用别的方法证明,如勾股定理逆定理;(Ⅲ)求直线与平面所成的角,根据其定义,应作出这条直线在平面中的射影,再求这条直线与其射影的夹角(三角函数值),本题可考虑点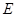 在平面
在平面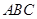 的射影,易知平面
的射影,易知平面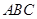 与侧面
与侧面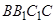 垂直,所以点
垂直,所以点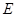 在平面
在平面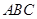 的射影必在两平面的交线上,过
的射影必在两平面的交线上,过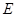 做
做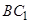 的垂线交
的垂线交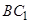 于
于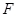 ,则
,则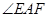 为所求的直线与平面的夹角.
为所求的直线与平面的夹角.试题解析:(Ⅰ)因为
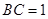 ,
,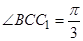 ,
,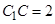 ,所以
,所以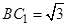 ,
,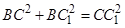 ,所以
,所以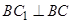
因为
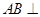 侧面
侧面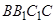 ,
,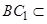 平面
平面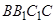 ,所以
,所以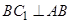 ,又
,又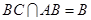 ,
,所以,
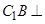 平面
平面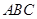 4分
4分(Ⅱ)取
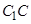 的中点
的中点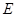 ,连接
,连接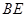 ,
,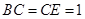 ,
,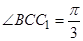 ,等边
,等边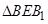 中,
中,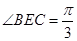
同理,
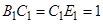 ,
, 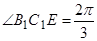 ,所以
,所以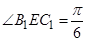 ,可得
,可得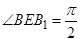 ,所以
,所以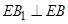
因为
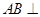 侧面
侧面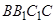 ,
,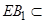 平面
平面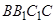 ,所以
,所以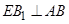 ,且
,且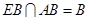 ,
,所以
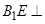 平面
平面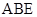 ,所以
,所以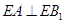 ; 8分
; 8分(Ⅲ)
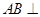 侧面
侧面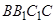 ,
,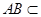 平面,得平面
平面,得平面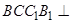 平面
平面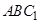 ,
,过
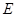 做
做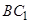 的垂线交
的垂线交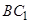 于
于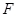 ,
,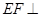 平面
平面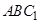
连接
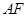 ,则
,则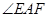 为所求,
为所求,因为
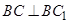 ,
,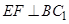 ,所以
,所以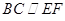 ,
,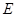 为
为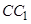 的中点 得
的中点 得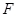 为
为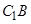 的中点,
的中点,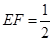 , 由(2)知
, 由(2)知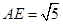 ,所以
,所以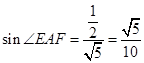 13分
13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
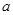 的正方体截去一半(如图甲所示)得到如图乙所示的几何体,点
的正方体截去一半(如图甲所示)得到如图乙所示的几何体,点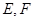 分别是
分别是 的中点.
的中点.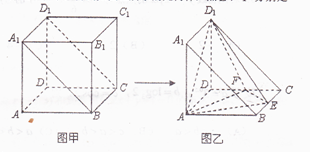
 ;
;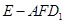 的体积.
的体积.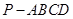 中,平面
中,平面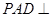 平面
平面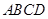 ,
,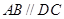 ,
,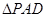 是等边三角形,已知
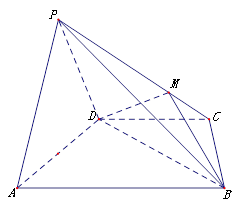
是等边三角形,已知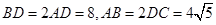 .
.
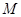 是
是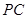 上的一点,证明:平面
上的一点,证明:平面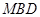 ;
;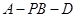 的余弦值.
的余弦值.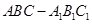 中,
中,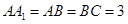 ,
,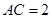 ,
,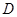 是
是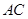 的中点.
的中点.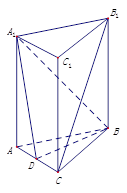
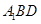 平面
平面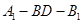 的余弦值.
的余弦值.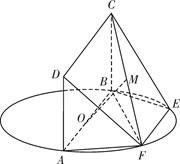
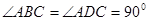 ,
,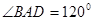 ,AD=AB=1,AC和BD交于O点.
,AD=AB=1,AC和BD交于O点.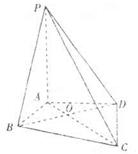
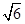 、 3,则这个三棱锥的外接球的表面积为 ( )
、 3,则这个三棱锥的外接球的表面积为 ( ) B.
B. C.
C.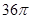 D.
D.