题目内容
设f(x)是(-∞,+∞)上的奇函数,对任意实数x,都有f(x+2)=-f(x),当-1≤x≤1时,f(x)=x3.(1)试证:x=1是函数f(x)的一条对称轴;
(2)证明函数f(x)是以4为周期的函数,并求x∈[1,5]时,f(x)的解析式.
解;(1)因为f(x)为奇函数,∴-f(x)=f(-x),又f(x+2)=f(-x),
∴f[(x-1)+2]=f[-(x-1)].
∴f(x+1)=f(1-x),
∴x=1是函数f(x)的一条对称轴.
(2)∵f(x+4)=-f(x+2)=f(x),
∴f(x)是以4为周期的函数.
又-1≤x≤1时,f(x)=x3.
当x∈[1,3],
∴x-2∈[-1,1],
∴f(x)=f(x-2+2)=-f(x-2)=-(x-2)3,
当x∈[3,5],
∴x-4∈[-1,1],
∴f(x)=f(x-4+4)=f(x-4)=(x-4)3;
∴x∈[1,5]时,f(x)的解析式为f(x)=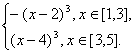

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 则f(
则f( 恒成立,则不等式
恒成立,则不等式 的解集是
的解集是