题目内容
15．计算：设a、b、c是非零实数，求$\frac{ab}{|ab|}$+$\frac{bc}{|bc|}$+$\frac{ac}{|ac|}$+$\frac{abc}{|abc|}$的值．分析 对a，b，c与0 的大小关系分类讨论，即可得出．
解答 解：①a，b，c＞0，则原式=1+1+1+1=4；
②a，b，c中只有一个大于0，不妨设a＞0，b，c＜0，则原式=-1+1-1+1=0；
③a，b，c中只有两个大于0，不妨设a，b＞0，c＜0，则原式=1-1-1-1=-2；
④a，b，c＜0，则原式=1+1+1-1=2．
点评 本题考查了分类讨论思想方法、绝对值的意义，考查了计算能力，属于基础题．
练习册系列答案
相关题目
选修4—4：坐标系与参数方程
在直角坐标系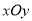
中，曲线
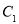的参数方程为
（
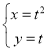为参数），以坐标原点为极点，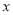
轴正半轴为极轴建立极坐标系，曲线
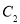的极坐标方程为
．
（1）把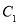
的参数方程化为极坐标方程 ；
（2）求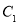
与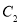
交点的极坐标（
）
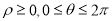4．已知函数f（x）的定义域是[0，2]，则函数g（x）=f（x+$\frac{1}{2}$）+f（x-$\frac{1}{2}$）的定义域是（ ）
| A． | [0，2] | B． | [$-\frac{1}{2}$，$\frac{3}{2}$] | C． | [$\frac{1}{2}$，$\frac{5}{2}$] | D． | [$\frac{1}{2}$，$\frac{3}{2}$] |