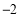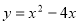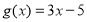Question

已知函数的图象的一个最高点为与之相邻的与轴的一个交点为

（1）求函数的解析式；

（2）求函数的单调减区间和函数图象的对称轴方程；

（3）用“五点法”作出函数在长度为一个周期区间上的图象.

 

Answer 1

（1）

（2），.

（3）见解析

【解析】

试题分析：⑴有最高点与相邻轴交点可知值，即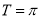，代入最高点求得值（注意尽量避免代入零点，若代零点需根据走向确定是的奇数倍还是偶数倍；（2）利用整体思想,;(3)找特殊点即使得为最值和零点的的值.

试题解析：⑴由题意，，，所以，所以，． 2分

所以，将代入，得，

因为，所以， 4分

所求函数解析式为． 5分

⑵由，得，

所以函数的单调减区间是． 7分

由（Z），得，

所以函数图象的对称轴方程为． 9分

⑶

1）列表

x
	0
y	0	2		0	2

13分

2）描点画图

16分

考点：1.求三角函数解析式；2.三角函数的性质；3.五点作图法.