题目内容
已知双曲线的一条渐近线方程是y=
x,焦距为2
,则此双曲线的标准方程为
-
=1或
-
=1
-
=1或
-
=1.
| ||
| 2 |
| 7 |
| x2 |
| 4 |
| y2 |
| 3 |
| y2 |
| 3 |
| x2 |
| 4 |
| x2 |
| 4 |
| y2 |
| 3 |
| y2 |
| 3 |
| x2 |
| 4 |
分析:若双曲线焦点在x轴上,设它的标准方程为
-
=1(a>0,b>0).根据渐近线方程是y=
x,可得
=
,再根据焦距为2
,得到c=
=
,联解可得a2和b2的值,从而得到焦点在x轴上双曲线的标准方程.然后用类似的方法,可得焦点在y轴上双曲线的标准方程,最后得到满足题意的双曲线的标准方程.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| b |
| a |
| ||
| 2 |
| 7 |
| a2+b2 |
| 7 |
解答:解:(1)当双曲线焦点在x轴上时,
设它的标准方程为
-
=1(a>0,b>0)
∵双曲线的一条渐近线方程是y=
x,
∴渐近线方程y=±
x即y=±
x,有
=
…①
又∵双曲线的焦距为2
∴c=
=
…②
联解①②,得a2=4,b2=3
∴双曲线方程为
-
=1
(2)当双曲线焦点在y轴上时,
设它的标准方程为
-
=1(a>0,b>0)
采用类似(1)的方法,可得a2=3,b2=4
∴双曲线方程为
-
=1
综上所述,所求双曲线方程为:
-
=1或
-
=1
故答案为:
-
=1或
-
=1
设它的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
∵双曲线的一条渐近线方程是y=
| ||
| 2 |
∴渐近线方程y=±
| b |
| a |
| ||
| 2 |
| b |
| a |
| ||
| 2 |
又∵双曲线的焦距为2
| 7 |
∴c=
| a2+b2 |
| 7 |
联解①②,得a2=4,b2=3
∴双曲线方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)当双曲线焦点在y轴上时,
设它的标准方程为
| y2 |
| a2 |
| x2 |
| b2 |
采用类似(1)的方法,可得a2=3,b2=4
∴双曲线方程为
| y2 |
| 3 |
| x2 |
| 4 |
综上所述,所求双曲线方程为:
| x2 |
| 4 |
| y2 |
| 3 |
| y2 |
| 3 |
| x2 |
| 4 |
故答案为:
| x2 |
| 4 |
| y2 |
| 3 |
| y2 |
| 3 |
| x2 |
| 4 |
点评:本题用待定系数法求双曲线的标准方程,着重考查了双曲线的渐近线和焦点等基本概念和双曲线的简单性质,属于基础题.

练习册系列答案
相关题目
 -
- =1(a>0,b>0)的左顶点,且此双曲线的一条渐
=1(a>0,b>0)的左顶点,且此双曲线的一条渐 B.2
B.2 D.2
D.2 分别是双曲线
分别是双曲线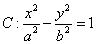
 的左,右焦点。过点
的左,右焦点。过点 与双曲线的一条渐
与双曲线的一条渐 ,且
,且 ,则双曲线的离心率为( )
,则双曲线的离心率为( ) (B)
(B) 
 (D)
(D)
