题目内容
若关于x的方程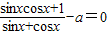 在
在 内恰有两实数解,则实数a的取值范围为 .
内恰有两实数解,则实数a的取值范围为 .
【答案】分析:令sinx+cosx=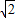 sin(x+
sin(x+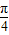 )=t,则得 t∈[-
)=t,则得 t∈[- ,0),a=
,0),a= =
= ,再利用基本不等式求出实数a的取值范围.
,再利用基本不等式求出实数a的取值范围.
解答:解:令sinx+cosx=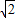 sin(x+
sin(x+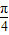 )=t,则有 sinxcosx=
)=t,则有 sinxcosx=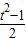 .
.
∵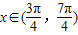 ,∴π≤x+
,∴π≤x+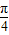 ≤2π,-1≤sin(x+
≤2π,-1≤sin(x+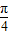 )≤0.
)≤0.
结合题意可得 t∈[-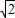 ,0),故
,0),故 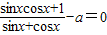 即
即 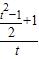 =a,即 a=
=a,即 a=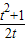 =
= .
.
∴-a=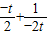 ≥2
≥2 =1,当且仅当
=1,当且仅当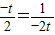 ,即 t=-1时,等号成立,故a≤-1,.
,即 t=-1时,等号成立,故a≤-1,.
当t∈(-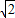 ,0)时,每一个t值,对应了满足 π≤x+
,0)时,每一个t值,对应了满足 π≤x+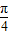 ≤2π 的2个x值(x+
≤2π 的2个x值(x+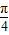 可能在第三象限,也可能在第四象限),
可能在第三象限,也可能在第四象限),
故答案为 (-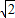 ,-1].
,-1].
点评:本题主要考查三角函数的恒等变换以及基本不等式的应用,注意检验等号成立的条件,式子的变形是解题的关键,属于中档题.
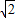 sin(x+
sin(x+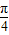 )=t,则得 t∈[-
)=t,则得 t∈[- ,0),a=
,0),a= =
= ,再利用基本不等式求出实数a的取值范围.
,再利用基本不等式求出实数a的取值范围.解答:解:令sinx+cosx=
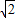 sin(x+
sin(x+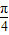 )=t,则有 sinxcosx=
)=t,则有 sinxcosx=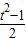 .
.∵
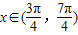 ,∴π≤x+
,∴π≤x+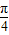 ≤2π,-1≤sin(x+
≤2π,-1≤sin(x+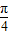 )≤0.
)≤0.结合题意可得 t∈[-
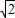 ,0),故
,0),故 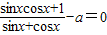 即
即 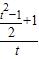 =a,即 a=
=a,即 a=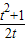 =
= .
.∴-a=
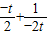 ≥2
≥2 =1,当且仅当
=1,当且仅当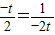 ,即 t=-1时,等号成立,故a≤-1,.
,即 t=-1时,等号成立,故a≤-1,.当t∈(-
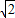 ,0)时,每一个t值,对应了满足 π≤x+
,0)时,每一个t值,对应了满足 π≤x+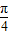 ≤2π 的2个x值(x+
≤2π 的2个x值(x+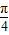 可能在第三象限,也可能在第四象限),
可能在第三象限,也可能在第四象限),故答案为 (-
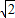 ,-1].
,-1].点评:本题主要考查三角函数的恒等变换以及基本不等式的应用,注意检验等号成立的条件,式子的变形是解题的关键,属于中档题.

练习册系列答案
相关题目