题目内容
设 为奇函数,
为奇函数, 为常数.
为常数.
(Ⅰ)求 的值; (Ⅱ)判断
的值; (Ⅱ)判断 在区间(1,+∞)的单调性,并说明理由;
在区间(1,+∞)的单调性,并说明理由;
(Ⅲ)若对于区间[3,4]上的每一个 值,不等式
值,不等式 >
> 恒成立,求实数
恒成立,求实数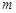 的取值范围.
的取值范围.
 为奇函数,
为奇函数, 为常数.
为常数.(Ⅰ)求
 的值; (Ⅱ)判断
的值; (Ⅱ)判断 在区间(1,+∞)的单调性,并说明理由;
在区间(1,+∞)的单调性,并说明理由;(Ⅲ)若对于区间[3,4]上的每一个
 值,不等式
值,不等式 >
> 恒成立,求实数
恒成立,求实数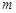 的取值范围.
的取值范围.(Ⅰ)∵ f(-x)=-f(x) ∴ ……1分
……1分
∴ ,即
,即
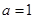 不合题意 ……3分
不合题意 ……3分
∴a=-1 ……4分
(Ⅱ)由(1)可知f(x)=
 (x>1) ……5分
(x>1) ……5分
记u(x)=1+ ,由定义可证明u(x)在
,由定义可证明u(x)在 上为减函数 ……7分
上为减函数 ……7分
∴ f(x)= 在
在 上为增函数 ……8分
上为增函数 ……8分
(其他解法参照给分)
(Ⅲ)设g(x)= -
- .则g(x)在[3,4]上为增函数 ……9分
.则g(x)在[3,4]上为增函数 ……9分
∴g(x)>m对x∈[3,4]恒成立,∴ ……10
……10
又g(3)=- ……11分
……11分 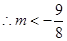
 ……1分
……1分∴
 ,即
,即
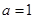 不合题意 ……3分
不合题意 ……3分∴a=-1 ……4分
(Ⅱ)由(1)可知f(x)=

 (x>1) ……5分
(x>1) ……5分记u(x)=1+
 ,由定义可证明u(x)在
,由定义可证明u(x)在 上为减函数 ……7分
上为减函数 ……7分∴ f(x)=
 在
在 上为增函数 ……8分
上为增函数 ……8分 (其他解法参照给分)
(Ⅲ)设g(x)=
 -
- .则g(x)在[3,4]上为增函数 ……9分
.则g(x)在[3,4]上为增函数 ……9分∴g(x)>m对x∈[3,4]恒成立,∴
 ……10
……10又g(3)=-
 ……11分
……11分 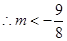
略

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 ,
, ,且
,且 ,则( )
,则( )



 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
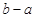 ).
).
 在
在 上为减函数,求
上为减函数,求 的取值范围;
的取值范围; 时,求
时,求 的值域;
的值域; 的方程
的方程 在
在 上仅有一解,求实数
上仅有一解,求实数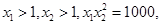 则
则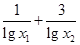 的最小值为
的最小值为 


 ;
; ,求
,求 的值。
的值。 (1)
(1)

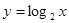 的图象上有三个点A,B,C,它们的横坐标依次为
的图象上有三个点A,B,C,它们的横坐标依次为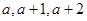 ,其中
,其中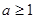 .设△
.设△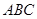 的面积为S.
的面积为S.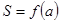 ;
; ,那么
,那么 用
用 表示是
表示是 


