题目内容
设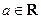 ,函数
,函数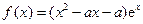 .
.
(Ⅰ)若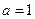 ,求曲线
,求曲线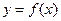 在点
在点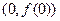 处的切线方程;
处的切线方程;
(Ⅱ)求函数 在
在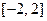 上的最小值.
上的最小值.
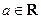 ,函数
,函数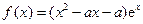 .
.(Ⅰ)若
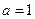 ,求曲线
,求曲线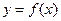 在点
在点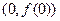 处的切线方程;
处的切线方程;(Ⅱ)求函数
 在
在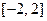 上的最小值.
上的最小值.(Ⅰ)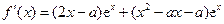
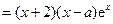 .
.
当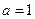 时,
时,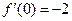 ,
,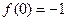 ,所以曲线
,所以曲线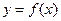 在点
在点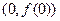 处的切线方程为
处的切线方程为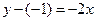 ,即
,即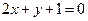 .
.
(Ⅱ)令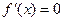 ,解得
,解得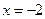 或
或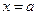 .
.
①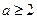 ,则当
,则当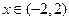 时,
时,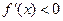 ,函数
,函数 在
在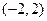 上单调递减,
上单调递减,
所以,当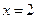 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为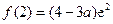 .
.
②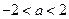 ,则当
,则当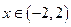 时,当
时,当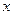 变化时,
变化时,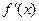 ,
, 的变化情况如下表:
的变化情况如下表:
所以,当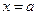 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为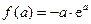 .
.
③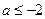 ,则当
,则当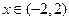 时,
时,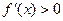 ,函数
,函数 在
在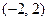 上单调递增,
上单调递增,
所以,当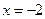 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为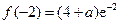 .
.
综上,当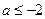 时,
时, 的最小值为
的最小值为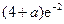 ;当
;当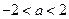 时,
时, 的最小值为
的最小值为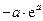 ;
;
当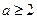 时,
时, 的最小值为
的最小值为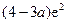 .
.
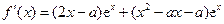
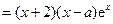 .
. 当
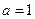 时,
时,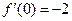 ,
,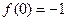 ,所以曲线
,所以曲线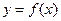 在点
在点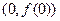 处的切线方程为
处的切线方程为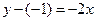 ,即
,即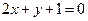 .
. (Ⅱ)令
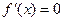 ,解得
,解得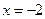 或
或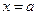 .
.①
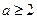 ,则当
,则当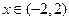 时,
时,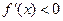 ,函数
,函数 在
在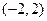 上单调递减,
上单调递减,所以,当
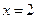 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为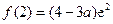 .
. ②
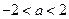 ,则当
,则当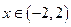 时,当
时,当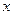 变化时,
变化时,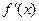 ,
, 的变化情况如下表:
的变化情况如下表: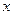 | 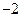 | 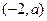 | 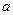 | 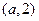 | 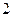 |
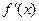 | | 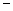 | 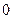 | 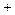 | |
 | 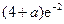 | 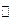 | 极小值 | 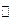 | 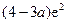 |
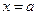 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为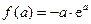 .
. ③
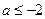 ,则当
,则当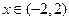 时,
时,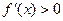 ,函数
,函数 在
在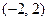 上单调递增,
上单调递增,所以,当
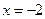 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为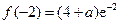 .
. 综上,当
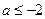 时,
时, 的最小值为
的最小值为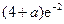 ;当
;当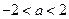 时,
时, 的最小值为
的最小值为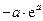 ;
;当
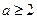 时,
时, 的最小值为
的最小值为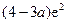 .
. 略

练习册系列答案
相关题目
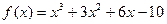 的切线中,斜率最小的切线方程为 ( )
的切线中,斜率最小的切线方程为 ( )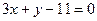
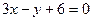
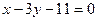
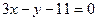
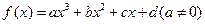 的导函数是
的导函数是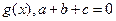 ,
,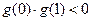 . 设
. 设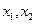 是方程
是方程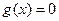 的两根,则|
的两根,则|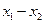 |的取值范围为 .
|的取值范围为 .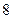 米,一个身高为
米,一个身高为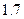 米的人以每秒
米的人以每秒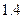 米的速度匀速地从路灯的正下方沿某直线离开路灯,那么人影长度的变化率为 米/秒(精确到
米的速度匀速地从路灯的正下方沿某直线离开路灯,那么人影长度的变化率为 米/秒(精确到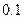 );
);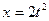 运动,则该质点在
运动,则该质点在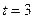 时的瞬时
时的瞬时 速度为 。
速度为 。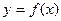 的图象如图,
的图象如图,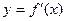 的草图为 ▲ .
的草图为 ▲ .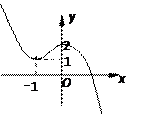
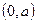 的直线与曲线
的直线与曲线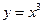 和
和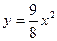 都相切,则
都相切,则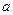 的值为
的值为 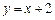 与曲线
与曲线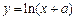 相切,则
相切,则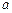 的值为 .
的值为 .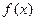 是以
是以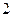 为周期的偶函数,且当
为周期的偶函数,且当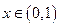 时,
时,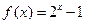 ,则
,则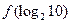 的值为( )
的值为( )