题目内容
曲线y=x2-3x上在点P处的切线平行于x轴,则P的坐标为( )
A、(-
| ||||
B、(
| ||||
C、(-
| ||||
D、(
|
分析:先对曲线求导,然后令导函数等于0即可求出横坐标,然后代入曲线即可得到答案.
解答:解:y′=2x-3,令y′=0.
即2x-3=0,得x=
.
代入曲线方程y=x2-3x,
得y=-
.
故选B.
即2x-3=0,得x=
| 3 |
| 2 |
代入曲线方程y=x2-3x,
得y=-
| 9 |
| 4 |
故选B.
点评:本题主要考查导数的几何意义,即函数在某点的导数值等于过该点切线的斜率.

练习册系列答案
相关题目
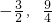 )
)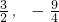 )
)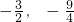 )
)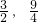 )
)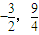 )
) )
) )
)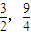 )
)