题目内容
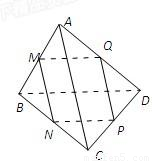
如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
求证:(1)线段MP和NQ相交且互相平分;
(2)AC∥平面MNP,BD∥平面MNP.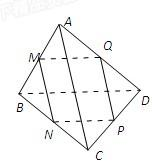
求证:(1)线段MP和NQ相交且互相平分;
(2)AC∥平面MNP,BD∥平面MNP.

证明:(1)∵M、N是AB、BC的中点,∴MN∥AC,MN=
AC.
∵P、Q是CD、DA的中点,∴PQ∥CA,PQ=
CA.
∴MN∥QP,MN=QP,MNPQ是平行四边形.
∴□MNPQ的对角线MP、NQ相交且互相平分.
(2)由(1),AC∥MN.记平面MNP(即平面MNPQ)为α.显然AC?α.
否则,若AC?α,
由A∈α,M∈α,得B∈α;
由A∈α,Q∈α,得D∈α,则A、B、C、D∈α,
与已知四边形ABCD是空间四边形矛盾.
又∵MNìα,∴AC∥α,
又AC?α,∴AC∥α,即AC∥平面MNP.
又∵BD∥NP,BD?平面MNP,NP?平面MNP
∴BD∥平面MNP.
| 1 |
| 2 |
∵P、Q是CD、DA的中点,∴PQ∥CA,PQ=
| 1 |
| 2 |
∴MN∥QP,MN=QP,MNPQ是平行四边形.
∴□MNPQ的对角线MP、NQ相交且互相平分.
(2)由(1),AC∥MN.记平面MNP(即平面MNPQ)为α.显然AC?α.
否则,若AC?α,
由A∈α,M∈α,得B∈α;
由A∈α,Q∈α,得D∈α,则A、B、C、D∈α,
与已知四边形ABCD是空间四边形矛盾.
又∵MNìα,∴AC∥α,
又AC?α,∴AC∥α,即AC∥平面MNP.
又∵BD∥NP,BD?平面MNP,NP?平面MNP
∴BD∥平面MNP.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
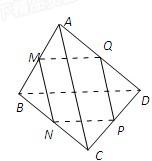 如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.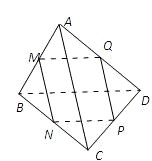 如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.