题目内容
练习:求数列
,
,
,…,
…前n项的和.
| 2 |
| 2 |
| 4 |
| 22 |
| 6 |
| 23 |
| 2n |
| 2n |
分析:结合数列的项的特点,考虑利用错位相减求和即可求解
解答:解:令S=
+
+
+…+
则
S=
+
+…+
+
两式相减可得,
S=1+2(
+
+…+
)-
=1+2×
-
=2-
-
∴s=4-
| 2 |
| 2 |
| 4 |
| 22 |
| 6 |
| 23 |
| 2n |
| 2n |
则
| 1 |
| 2 |
| 2 |
| 22 |
| 4 |
| 23 |
| 2n-2 |
| 2n |
| 2n |
| 2n+1 |
两式相减可得,
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 2n |
| 2n+1 |
| ||||
1-
|
| n |
| 2n |
| 1 |
| 2n-1 |
| n |
| 2n |
∴s=4-
| 2+n |
| 2n-1 |
点评:本题主要考查了错位相减法求和方法在数列求和中的简单应用,注意基本方法的掌握.

练习册系列答案
相关题目
 ,
,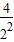 ,
, ,…,
,…,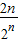 …前n项的和.
…前n项的和.