题目内容
已知函数 .
.(I)若曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直,求a的值;
(II)求函数f(x)的单调区间.
【答案】分析:(I)求得函数f(x)的定义域,求导函数,利用曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直,即可求a的值;
(II)由于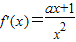 ,分类讨论,利用导数的正负,可得函数的单调区间.
,分类讨论,利用导数的正负,可得函数的单调区间.
解答:解:(I)函数f(x)的定义域为{x|x>0},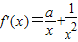 .
.
又曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直,所以f′(1)=a+1=2.解得a=1.
(II)由于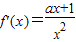 .
.
当a≥0时,对于x∈(0,+∞),有f′(x)>0在定义域上恒成立,即f(x)在(0,+∞)上是增函数.
当a<0时,由f′(x)=0,得x=-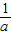 ∈(0,+∞);
∈(0,+∞);
当x∈(0,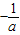 )时,f′(x)>0,f(x)单调递增;
)时,f′(x)>0,f(x)单调递增;
当x∈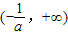 时,f′(x)<0,f(x)单调递减.
时,f′(x)<0,f(x)单调递减.
点评:本题考查导数知识的运用,考查函数的单调性,考查学生的计算能力,属于中档题.
(II)由于
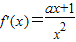 ,分类讨论,利用导数的正负,可得函数的单调区间.
,分类讨论,利用导数的正负,可得函数的单调区间.解答:解:(I)函数f(x)的定义域为{x|x>0},
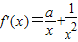 .
.又曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直,所以f′(1)=a+1=2.解得a=1.
(II)由于
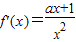 .
.当a≥0时,对于x∈(0,+∞),有f′(x)>0在定义域上恒成立,即f(x)在(0,+∞)上是增函数.
当a<0时,由f′(x)=0,得x=-
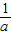 ∈(0,+∞);
∈(0,+∞);当x∈(0,
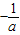 )时,f′(x)>0,f(x)单调递增;
)时,f′(x)>0,f(x)单调递增;当x∈
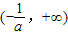 时,f′(x)<0,f(x)单调递减.
时,f′(x)<0,f(x)单调递减.点评:本题考查导数知识的运用,考查函数的单调性,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 .
. ,求实数a的值;
,求实数a的值;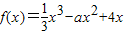 .
. ,求实数a的值;
,求实数a的值; .
. ,求实数a的值;
,求实数a的值; .
. ,求实数a的值;
,求实数a的值;