题目内容
(本小题9分)在△ABC中,∠A、∠B、∠C所对的边长分别为a、b、c,且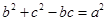 和
和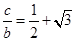 ,求∠A和
,求∠A和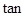 B 的值。
B 的值。
【答案】
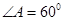 ,
,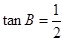 。
。
【解析】本试题主要是考查了解三角形的运用。利用余弦定理和正弦定理以及三角形的面积公式的综合运用。首先利用余弦定理和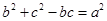 得到角A的值,然后利用
得到角A的值,然后利用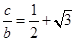 正弦定理得到B,C角的关系式,从而得到角B的正切值。
正弦定理得到B,C角的关系式,从而得到角B的正切值。
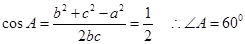
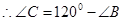
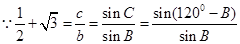
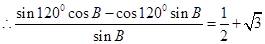
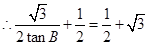
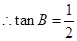

练习册系列答案
相关题目
 已知等轴双曲线C的两个焦点F1、F2在直线y=x上,线段F1F2的中点是坐标原点,且双曲线经过点(3,
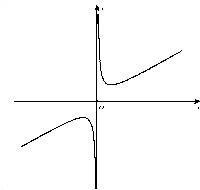
已知等轴双曲线C的两个焦点F1、F2在直线y=x上,线段F1F2的中点是坐标原点,且双曲线经过点(3,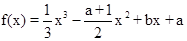 (a,b∈R),且其导函数f′ (x)的图象过原点.
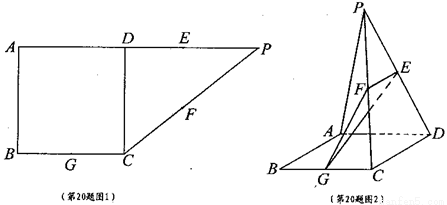
(a,b∈R),且其导函数f′ (x)的图象过原点.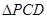 沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。