题目内容
如图,一个粒子在第一象限运动,在第一秒末,它从原点运动到(0,1),接着它按如图所示的x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…),且每秒移动一个单位,那么第2008秒末这个粒子所处的位置的坐标为 .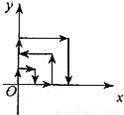
【答案】分析:该题显然是数列问题.设粒子运动到A1,A2,…An时所用的间分别为a1,a2,…an,则a1=2,a2=6,a3=12,a4=20,…,由an-an-1=2n,则a2-a1=2×2,a3-a2=2×3,a4-a3=2×4,…,an-an-1=2n,以上相加得到an-a1的值,进而求得an来解.
解答:解: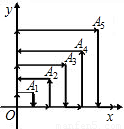 如右图所示,
如右图所示,
设粒子运动到A1,A2,…,An时所用的间分别为a1,a2,…,an,
则a1=2,a2=6,a3=12,a4=20,…,an-an-1=2n,
将a2-a1=2×2,a3-a2=2×3,a4-a3=2×4,…,an-an-1=2n相加得:
an-a1=2(2+3+4+…+n)=n2+n-2,
∴an=n(n+1).
44×45=1980,故运动了1980秒时它到点A44(44,44);又由运动规律知:A1,A2,…,An中,奇数点处向下运动,偶数点处向左运动.故达到A44(44,44)时向左运动28秒到达点(16,44),即运动了2008秒.所求点应为(16,44).
故答案为:(16,44)
点评:分析粒子在第一象限的运动规律得到数列{an}通项的递推关系式an-an-1=2n是本题的突破口,对运动规律的探索知:A1,A2,…An中,奇数点处向下运动,偶数点处向左运动是解题的关键.
解答:解:
 如右图所示,
如右图所示,设粒子运动到A1,A2,…,An时所用的间分别为a1,a2,…,an,
则a1=2,a2=6,a3=12,a4=20,…,an-an-1=2n,
将a2-a1=2×2,a3-a2=2×3,a4-a3=2×4,…,an-an-1=2n相加得:
an-a1=2(2+3+4+…+n)=n2+n-2,
∴an=n(n+1).
44×45=1980,故运动了1980秒时它到点A44(44,44);又由运动规律知:A1,A2,…,An中,奇数点处向下运动,偶数点处向左运动.故达到A44(44,44)时向左运动28秒到达点(16,44),即运动了2008秒.所求点应为(16,44).
故答案为:(16,44)
点评:分析粒子在第一象限的运动规律得到数列{an}通项的递推关系式an-an-1=2n是本题的突破口,对运动规律的探索知:A1,A2,…An中,奇数点处向下运动,偶数点处向左运动是解题的关键.

练习册系列答案
相关题目
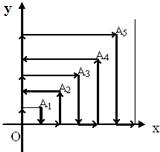 8、如图,一个粒子在第一象限运动,在第一秒内,它从原点运动到(0,1),然后接着按图所示在x轴,y轴平行方向来回运动(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0) …),若每秒运动一个单位长度,那么第2010秒时,这个粒子所在的位置为( )
8、如图,一个粒子在第一象限运动,在第一秒内,它从原点运动到(0,1),然后接着按图所示在x轴,y轴平行方向来回运动(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0) …),若每秒运动一个单位长度,那么第2010秒时,这个粒子所在的位置为( )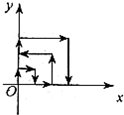 如图,一个粒子在第一象限运动,在第一秒末,它从原点运动到(0,1),接着它按如图所示的x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…),且每秒移动一个单位,那么第2008秒末这个粒子所处的位置的坐标为
如图,一个粒子在第一象限运动,在第一秒末,它从原点运动到(0,1),接着它按如图所示的x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…),且每秒移动一个单位,那么第2008秒末这个粒子所处的位置的坐标为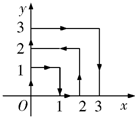 如图,一个粒子在第一象限及坐标轴上运动,在第一秒内它从原点运动到(0,1),然后它接着按图示在x轴、y轴的平行方向来回运动,且每秒移动一个单位长度,求2006秒时,这个粒子所处的位置.
如图,一个粒子在第一象限及坐标轴上运动,在第一秒内它从原点运动到(0,1),然后它接着按图示在x轴、y轴的平行方向来回运动,且每秒移动一个单位长度,求2006秒时,这个粒子所处的位置.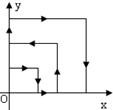
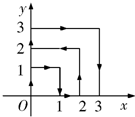 如图,一个粒子在第一象限及坐标轴上运动,在第一秒内它从原点运动到(0,1),然后它接着按图示在x轴、y轴的平行方向来回运动,且每秒移动一个单位长度,求2006秒时,这个粒子所处的位置.
如图,一个粒子在第一象限及坐标轴上运动,在第一秒内它从原点运动到(0,1),然后它接着按图示在x轴、y轴的平行方向来回运动,且每秒移动一个单位长度,求2006秒时,这个粒子所处的位置.