Question

已知椭圆C中心在原点，焦点在x轴上，离心率e=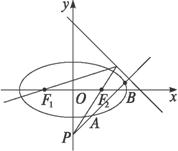，光线从点P(0,-3)出发经过右焦点F₂，到直线：x+y-2=0后被它反射，反射光线经过左焦点F₁.

（1）求椭圆C的方程；

（2）经过P的直线l与椭圆C相交于A，B，D（0,m）为y轴上一点，若=0，求m的取值范围.

Answer 1

解：（1）设椭圆C的方程为=1(a＞b＞0),点F₂,P关于直线：x+y-2=0的对称点E，P′的坐标分别为(2,2-c),(5,2)，则点P′,E,F₁三点共线，

∴，c²+5c-6=0，(c＞0)

∴c=1,又椭圆的离心率e=，

∴a=2,b=1，椭圆C的方程为+y²=1.

（2）因为=0，所以，D是线段AB的中垂线与y轴的交点，设：A(x₁,y₁)，B(x₂,y₂),AB的中点M(x₀,y₀)，直线l的斜率为k，则有

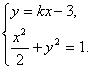消去y得(1+2k²)x²-12kx+16=0，

∴∴x₀=,y₀=kx₀-3=.

线段AB的中垂线方程为y+=-(x-)，

∴m=.

∵Δ=144k²-64(1+2k²)=16k²-64＞0,

∴1+2k²＞90＜m＜

又当l⊥x轴时，m=0,∴0≤m＜