题目内容
求圆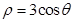 被直线
被直线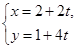 (
( 是参数)截得的弦长.
是参数)截得的弦长.
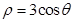 被直线
被直线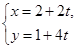 (
( 是参数)截得的弦长.
是参数)截得的弦长.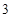 .
.试题分析:先将圆
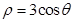 极坐标方程及直线
极坐标方程及直线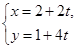 参数方程转化成直角坐标方程,然后利用垂径定理及勾股定理求弦长.
参数方程转化成直角坐标方程,然后利用垂径定理及勾股定理求弦长.试题解析:将圆的极坐标方程转化成直角坐标方程:
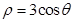 即:
即: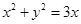 ,即
,即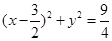 ; 2分
; 2分而直线
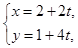 即:
即: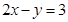 , 4分
, 4分由于圆心
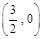 到直线
到直线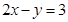 的距离
的距离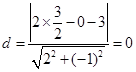 , 6分
, 6分即直线经过圆心,所以圆被直线截得的弦长为
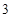 . 7分
. 7分
练习册系列答案
相关题目
题目内容
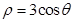 被直线
被直线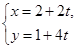 (
( 是参数)截得的弦长.
是参数)截得的弦长.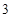 .
.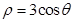 极坐标方程及直线
极坐标方程及直线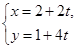 参数方程转化成直角坐标方程,然后利用垂径定理及勾股定理求弦长.
参数方程转化成直角坐标方程,然后利用垂径定理及勾股定理求弦长.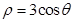 即:
即: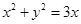 ,即
,即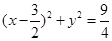 ; 2分
; 2分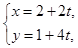 即:
即: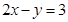 , 4分
, 4分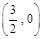 到直线
到直线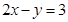 的距离
的距离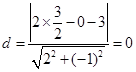 , 6分
, 6分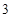 . 7分
. 7分