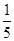题目内容
一个椭圆的长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是
.
| 3 |
| 5 |
| 3 |
| 5 |
分析:由题意可得,2b=a+c,平方可得4b2=a2+2ac+c2结合b2=a2-c2可得关于a,c的二次方程,然后由e=
及0<e<1可求
| c |
| a |
解答:解:由题意可得,2a,2b,2c成等差数列
∴2b=a+c
∴4b2=a2+2ac+c2①
∵b2=a2-c2②
①②联立可得,5c2+2ac-3a2=0
∵e=
∴5e2+2e-3=0
∵0<e<1
∴e=
故答案为:
∴2b=a+c
∴4b2=a2+2ac+c2①
∵b2=a2-c2②
①②联立可得,5c2+2ac-3a2=0
∵e=
| c |
| a |
∴5e2+2e-3=0
∵0<e<1
∴e=
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
点评:本题主要考查了椭圆的性质的应用,解题中要椭圆离心率的取值范围的应用,属于中档试题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
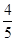 B.
B.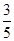 C.
C.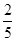 D.
D.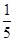
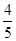 B.
B.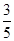 C.
C.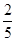 D.
D.
 B.
B. C.
C. D.
D.