题目内容
某校要建造一个容积为8m3,深为2m的长方体无盖水池,池底和池壁的造价每平方米分别为240元和160元,那么水池的最低总造价为
3520
3520
元.分析:设底面一边长x(m),那么令一边长为
(m),底面积为4,侧面积为2×2x+2×
,这样,可得总造价y,再利用基本不等式,可求得水池的最低总造价
| 4 |
| x |
| 8 |
| x |
解答: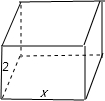 解:设底面一边长x(m),那么另一边长为
解:设底面一边长x(m),那么另一边长为
(m),如图:
总造价为:y=(2×2x+2×
)×160+4×240=(x+
)×640+960
≥2
×640+960=3520元
当且仅当x=
,即x=2时,函数y的值最小,即当底面边长为2(m)的正方形时,建造的水池造价最少.
故答案为:3520
 解:设底面一边长x(m),那么另一边长为
解:设底面一边长x(m),那么另一边长为| 4 |
| x |
总造价为:y=(2×2x+2×
| 8 |
| x |
| 4 |
| x |
≥2
x×
|
当且仅当x=
| 4 |
| x |
故答案为:3520
点评:本题考查了长方形模型的应用,由长方形的侧面积建立函数解析式,由解析式判断单调性并求最值,是中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
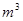 ,深为2
,深为2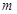 的长方体无盖水池,池底和池壁的造价每平方米分别为240元和160元,那么水池的最低总造价为
元。
的长方体无盖水池,池底和池壁的造价每平方米分别为240元和160元,那么水池的最低总造价为
元。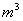 ,深为2
,深为2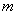 的长方体无盖水池,池底和池壁的造价每平方米分别为240元和160元,那么水池的最低总造价为
元。
的长方体无盖水池,池底和池壁的造价每平方米分别为240元和160元,那么水池的最低总造价为
元。