题目内容
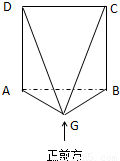
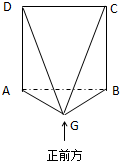 (文)已知在四棱锥G-ABCD中,(如图)ABCD是正方形,且边长为2,正前方ABCDG面ABCD⊥面ABG,AG=BG.
(文)已知在四棱锥G-ABCD中,(如图)ABCD是正方形,且边长为2,正前方ABCDG面ABCD⊥面ABG,AG=BG.( I)在四棱锥G-ABCD中,过点B作平面AGC的垂线,若垂足H在CG上,求证:面AGD⊥面BGC
( II)在( I)的条件下,求三棱锥D-ACG的体积及其外接球的表面积.
分析:(I)由ABCD是正方形,面ABCD⊥面ABG,由面面垂直的性质可得BC⊥面ABG,则BC⊥AG,又由BH⊥面AGC得BH⊥AG,由线面垂直的判定定理可得AG⊥面AGD后,可由面面垂直的判定定理得到面AGD⊥面BGC
(II)△ABG中AG⊥BG且AG=BG,取AB中点E,连接GE,则GE⊥AB,利用等积法可得VD-ACG=VG-ACD=
GE•S△ACD,取AC中点M,可证得M即为三棱锥D-ACG的外接球的球心,求出球半径后,代入球的表面积公式,可得答案.
(II)△ABG中AG⊥BG且AG=BG,取AB中点E,连接GE,则GE⊥AB,利用等积法可得VD-ACG=VG-ACD=
| 1 |
| 3 |
解答: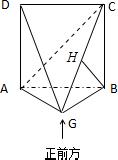 证明:(I)ABCD是正方形
证明:(I)ABCD是正方形
∴BC⊥AB
∵面ABCD⊥面ABG
∴BC⊥面ABG …2分
∵AG?面ABG
∴BC⊥AG
又BH⊥面AGC
∴BH⊥AG…4分
又∵BC∩BH=B
∴AG⊥面AGD
∴面AGD⊥面BGC …6分
( II)由( I)知 AG⊥面BGC
∴AG⊥BG
又AG=BG
∴△ABG是等腰Rt△,取AB中点E,连接GE,则GE⊥AB
∴GE⊥面ABCD
∴VD-ACG=VG-ACD=
GE•S△ACD=
•
•2a•
(2a)2=
a3 …8分
又AG⊥GC
∴取AC中点M,则MG=
AC
因此:MG=MA=MC=MD=
a
即点M是三棱锥D-ACG的外接球的球心,
半径为
a
∴三棱锥D-ACG的外接球的表面积S=4πR2=8πa2 …12分.
 证明:(I)ABCD是正方形
证明:(I)ABCD是正方形∴BC⊥AB
∵面ABCD⊥面ABG
∴BC⊥面ABG …2分
∵AG?面ABG
∴BC⊥AG
又BH⊥面AGC
∴BH⊥AG…4分
又∵BC∩BH=B
∴AG⊥面AGD
∴面AGD⊥面BGC …6分
( II)由( I)知 AG⊥面BGC
∴AG⊥BG
又AG=BG
∴△ABG是等腰Rt△,取AB中点E,连接GE,则GE⊥AB
∴GE⊥面ABCD
∴VD-ACG=VG-ACD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
又AG⊥GC
∴取AC中点M,则MG=
| 1 |
| 2 |
因此:MG=MA=MC=MD=
| 2 |
即点M是三棱锥D-ACG的外接球的球心,
半径为
| 2 |
∴三棱锥D-ACG的外接球的表面积S=4πR2=8πa2 …12分.
点评:本题考查的知识点是平面与平面垂直的判定,球的表面积,其中(1)要熟练掌握空间中线线垂直,线面垂直及面面垂直之间的相互转化,(2)的关键是等积法及球半径的求解.

练习册系列答案
相关题目