题目内容
已知函数 的图象关于直线
的图象关于直线 对称,则
对称,则 的单调递增区间为 .
的单调递增区间为 .
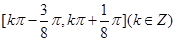
解析试题分析:因为函数 图象的对称轴为
图象的对称轴为 ,所以
,所以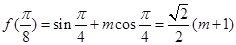 也就是函数的最值
也就是函数的最值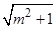 ,
,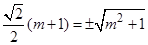 ,解得
,解得 ,所以
,所以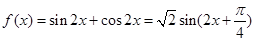 ,
,
由不等式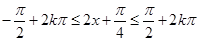 得
得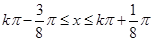 ,所以函数的递增区间为
,所以函数的递增区间为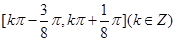 .
.
考点:三角函数的图象与性质.

练习册系列答案
相关题目
题目内容
已知函数 的图象关于直线
的图象关于直线 对称,则
对称,则 的单调递增区间为 .
的单调递增区间为 .
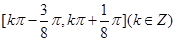
解析试题分析:因为函数 图象的对称轴为
图象的对称轴为 ,所以
,所以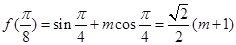 也就是函数的最值
也就是函数的最值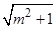 ,
,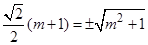 ,解得
,解得 ,所以
,所以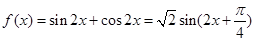 ,
,
由不等式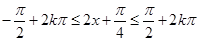 得
得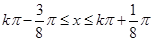 ,所以函数的递增区间为
,所以函数的递增区间为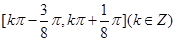 .
.
考点:三角函数的图象与性质.
