题目内容
(浙江卷理20文22)已知曲线C是到点P(-![]() ,
,![]() )和到直线y=-
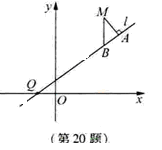
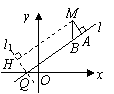
)和到直线y=-![]() 距离相等的点的轨迹.L是过点Q(-1,0)的直线,M是C上(不在l上)的动点; A、B在l上,MA
距离相等的点的轨迹.L是过点Q(-1,0)的直线,M是C上(不在l上)的动点; A、B在l上,MA![]() l,MB
l,MB![]() x轴(如图).
x轴(如图). 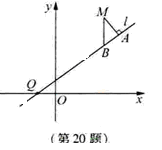
(Ⅰ)求曲线C的方程;
(Ⅱ)求出直线l的方程,使得![]() 为常数
为常数
. 本题主要考查求曲线的轨迹方程、两条直线的位置关系等基础知识,考查解析几何的基本思想方法和综合解题能力.满分15分.
(Ⅰ)解:设![]() 为
为![]() 上的点,则
上的点,则 ,
,
![]() 到直线
到直线![]() 的距离为
的距离为![]() .由题设得
.由题设得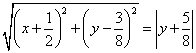 .
.
化简,得曲线![]() 的方程为
的方程为![]() .
.
(Ⅱ)解法一: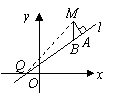 设
设 ,直线
,直线![]() ,则
,则
![]() ,从而
,从而![]() .
.
在![]() 中,因为
中,因为
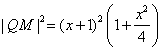 ,
,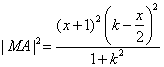 .
.
所以![]() .
.
![]() ,
,
 .
.
当![]() 时,
时,![]() ,从而所求直线
,从而所求直线![]() 方程为
方程为![]() .
.
解法二:设 ,直线
,直线![]() ,则
,则![]() ,从而
,从而
![]() .过
.过![]()
![]() 垂直于
垂直于![]() 的直线
的直线![]() .
.
 因为
因为![]() ,所以
,所以![]() ,
,
 .
.
当![]() 时,
时,![]() ,
,
从而所求直线![]() 方程为
方程为![]() .
.

练习册系列答案
相关题目