题目内容
直线 和
和 将圆
将圆 分成4部分,用5种不同颜色给四部分染色,每部分染一种颜色,相邻部分不能染同一种颜色,则不同的染色方案有
分成4部分,用5种不同颜色给四部分染色,每部分染一种颜色,相邻部分不能染同一种颜色,则不同的染色方案有
A 120种 B 240种 C 260种 D 280种
 和
和 将圆
将圆 分成4部分,用5种不同颜色给四部分染色,每部分染一种颜色,相邻部分不能染同一种颜色,则不同的染色方案有
分成4部分,用5种不同颜色给四部分染色,每部分染一种颜色,相邻部分不能染同一种颜色,则不同的染色方案有A 120种 B 240种 C 260种 D 280种
C
此题考查排列组合的问题
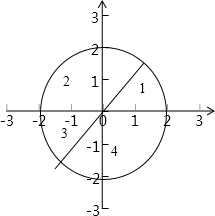
根据题意,直线x=0和y=-x将圆分成4部分,如图所示,设这4部分别为1、2、3、4号区域;
对于1号区域,有5种颜色可选,即有5种涂法,
分类讨论其他3个区域:①若2、4号区域涂不同的颜色,则有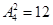 种涂法,3号区域有3种涂法,此时其他3个区域有12×3=36种涂法;
种涂法,3号区域有3种涂法,此时其他3个区域有12×3=36种涂法;
②若2、4号区域涂相同的颜色,则有4种涂法,3号区域有4种涂法,此时其他3个区域有有4×4=16种涂法;
则共有5×(36+16)=5×52=260种;
答案 C
点评:因为相邻部分不能同色,所以要分类讨论。
根据题意,直线x=0和y=-x将圆分成4部分,如图所示,设这4部分别为1、2、3、4号区域;
对于1号区域,有5种颜色可选,即有5种涂法,
分类讨论其他3个区域:①若2、4号区域涂不同的颜色,则有
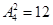 种涂法,3号区域有3种涂法,此时其他3个区域有12×3=36种涂法;
种涂法,3号区域有3种涂法,此时其他3个区域有12×3=36种涂法;②若2、4号区域涂相同的颜色,则有4种涂法,3号区域有4种涂法,此时其他3个区域有有4×4=16种涂法;
则共有5×(36+16)=5×52=260种;

答案 C
点评:因为相邻部分不能同色,所以要分类讨论。

练习册系列答案
相关题目
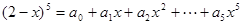 ,那么
,那么 的值为( )
的值为( ) B: -
B: - C:-
C:-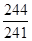 D:-1
D:-1 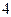 名学生和
名学生和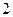 名教师站在一排照相,求:
名教师站在一排照相,求: 首尾不排教师,有多少种排法?
首尾不排教师,有多少种排法?
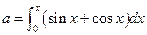 ,则二项式
,则二项式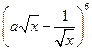 展开式中含
展开式中含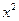 项的系数是 .
项的系数是 .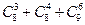 的值为 (用数字作答).
的值为 (用数字作答).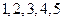 的五张卡片放入标有数字
的五张卡片放入标有数字