题目内容
袋中装有大小相同且质地一样的五个球,五个球上分别标有“2”,“3”,“4”,“6”,“9”这五个数.现从中随机选取三个球,则所选的三个球上的数恰好能构成等差数列或等比数列的概率是 .
【答案】分析:根据题意,能使所选的三个球上的数恰好能构成等差数列或等比数列的基本事件有4个,而所有的基本事件有 =10个,由此结合古典概型计算公式即可算出所求概率.
=10个,由此结合古典概型计算公式即可算出所求概率.
解答:解:取出的三个球上的数恰好能构成等差数列的情况有
“2,3,4”,“2,4,6”,“3,6,9”共3种取法;
恰好能构成等比数列的情况有:“4,6,9”,只有一种取法
∴所选的三个球上的数恰好能构成等差数列或等比数列的取法有:3+1=4种
而从五个球中任意取3个,共有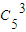 =10种不同取法,
=10种不同取法,
因此,所选的三个球上的数恰好能构成等差数列或等比数列的概率为:P=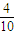 =
=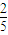
故答案为: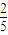
点评:本题给出“模球事件”,求取出的球成等差或等比数列的概率,着重考查了古典概型及其概率计算公式的知识,属于基础题.
 =10个,由此结合古典概型计算公式即可算出所求概率.
=10个,由此结合古典概型计算公式即可算出所求概率.解答:解:取出的三个球上的数恰好能构成等差数列的情况有
“2,3,4”,“2,4,6”,“3,6,9”共3种取法;
恰好能构成等比数列的情况有:“4,6,9”,只有一种取法
∴所选的三个球上的数恰好能构成等差数列或等比数列的取法有:3+1=4种
而从五个球中任意取3个,共有
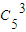 =10种不同取法,
=10种不同取法,因此,所选的三个球上的数恰好能构成等差数列或等比数列的概率为:P=
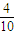 =
=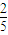
故答案为:
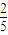
点评:本题给出“模球事件”,求取出的球成等差或等比数列的概率,着重考查了古典概型及其概率计算公式的知识,属于基础题.

练习册系列答案
相关题目