题目内容
设有两个命题,p:不等式|x|+|x+1|>a的解集为R;q:函数f(x)=-(7-3a)x在R上是减函数.如果这两个命题中有且只有一个是真命题,那么实数a的取值范围是( )A.1≤a<2 B.2<a≤![]() C.2≤a<
C.2≤a<![]() D.1<a≤2
D.1<a≤2
A
解析:由于函数f(x)=|x|+|x+1|的最小值为1,∴p为真时,a<1;而由函数f(x)=-(7-3a)x在R上是减函数可知7-3a>1,即a<2,∴q为真时,a<2,要使这两个命题中有且只有一个是真命题,必须![]() (p真q假时)或
(p真q假时)或![]() (p假q真时),可得1≤a<2.
(p假q真时),可得1≤a<2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
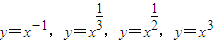 ,其中在R上是增函数的函数有3个.
,其中在R上是增函数的函数有3个.