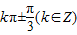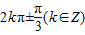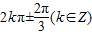Question

若数列1，2cosθ，2²cos²θ，2³cos³θ，…，前100项之和为0，则θ的值是（　　）

• A．kπ±

  π

  3

  (k∈Z)
• B．2kπ±

  π

  3

  (k∈Z)
• C．2kπ±

  2π

  3

  (k∈Z)
• D．以上答案均不对

Answer 1

分析：由题意可得，1，2cosθ，2²cos²θ，2³cos³θ，…为等比数列，由等比数列的前n项和公式可求，S₁₀₀=1+2cosθ+（2cosθ）²+…+（2cosθ）⁹⁹，从而可求θ

解答：解：∵1，2cosθ，2²cos²θ，2³cos³θ，…为等比数列，首项为1，公比为2cosθ
由等比数列的前n项和公式可得，
S₁₀₀=1+2cosθ+（2cosθ）²+…+（2cosθ）⁹⁹
=

1-(2cosθ)100

1-2cosθ

=0
由题意可得，

(2cosθ)100-1=0 1-2cosθ=0

∴2cosθ=-1 即cosθ=-

1

2

∴θ=2kπ±

2π

3

，k∈Z
故选：C

点评：本题主要考查了等比数列的前n项和公式在求解数列中的应用，解题的关键是求和后，要能利用三角函数的性质进行求解．