题目内容
若sin2x、sinx分别是sinθ与cosθ的等差中项和等比中项,则cos2x的值为:( )A.

B.

C.

D.

【答案】分析:利用等差中项和等比中项的性质求得sinx,sin2x与sinθ与cosθ的关系,进而利用同角三角函数的基本关系构造出等式,利用二倍角公式整理成关于cos2x的一元二次方程,解方程求得cos2x的值.
解答:解:依题意可知2sin2x=sinθ+cosθ
sin2x=sinθcosθ
∵sin2θ+cos2θ=(sinθ+cosθ)2-2sinθcosθ=4sin22x-2sin2x=1
∴4(1-cos22x)+cos2x-2=0,即4cos22x-cos2x-2=0,
求得cos2x=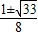
∵sin2x=sinθcosθ
∴cos2x=1-2sin2x=1-sin2θ≥0
∴cos2x=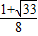
故选A.
点评:本题主要考查了三角函数的恒等变换及化简求值.解题的最后注意对cos2x的值进行验证,保证答案的正确性.
解答:解:依题意可知2sin2x=sinθ+cosθ
sin2x=sinθcosθ
∵sin2θ+cos2θ=(sinθ+cosθ)2-2sinθcosθ=4sin22x-2sin2x=1
∴4(1-cos22x)+cos2x-2=0,即4cos22x-cos2x-2=0,
求得cos2x=
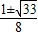
∵sin2x=sinθcosθ
∴cos2x=1-2sin2x=1-sin2θ≥0
∴cos2x=
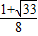
故选A.
点评:本题主要考查了三角函数的恒等变换及化简求值.解题的最后注意对cos2x的值进行验证,保证答案的正确性.

练习册系列答案
相关题目
若sin2x、sinx分别是sinθ与cosθ的等差中项和等比中项,则cos2x的值为:( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|