题目内容
 已知某职业技能培训班学生的项目A与项目B成绩抽样统计表如下,抽出学生n人,成绩只有3、4、5三种分值,设x,y分别表示项目A与项目B成绩.例如:表中项目A成绩为5分的共7+9+4=20人.已知x=4且y=5的概率是0.2.
已知某职业技能培训班学生的项目A与项目B成绩抽样统计表如下,抽出学生n人,成绩只有3、4、5三种分值,设x,y分别表示项目A与项目B成绩.例如:表中项目A成绩为5分的共7+9+4=20人.已知x=4且y=5的概率是0.2.(1)求n;
(2)若在该样本中,再按项目B的成绩分层抽样抽出20名学生,则y=3的学生中应抽多少人?
(3)已知a≥9,b≥2,项目B为3分的学生中,求项目A得3分的人数比得4分人数多的概率.
分析:(1)利用频率、频数的关系:频率=
即可求得n;
(2)由题意y=3的学生总人数为100-(7+20+5+9+18+6),据
=
即可求得y=3的学生中应抽多少人;
(3)由题意可知,满足条件的(a,b)的人数,再计算出b>a的人数,最后算出它们的比值即可.
| 频数 |
| 数据总和 |
(2)由题意y=3的学生总人数为100-(7+20+5+9+18+6),据
| 20 |
| 100 |
| m |
| 35 |
(3)由题意可知,满足条件的(a,b)的人数,再计算出b>a的人数,最后算出它们的比值即可.
解答:解:(1)由题意可知
=0.2,
得n=100人;(3分)
(2)由题意y=3的学生总人数为100-(7+20+5+9+18+6)=35,
设应在y=3的学生抽m人,则
=
,m=7人(7分)
(3)由题意可知a+b=35-4=31人,且a≥9,b≥2,
满足条件的(a,b)有(9,22),(10,21),(29,2),
共有21组,其中b>a的有7组. (9分)
记C表示时间“项目A得(3分)的人数比得(4分)人数多”
则P(C)=
=
. (11分)
答:(1)n=100人,(2)则y=3的学生中应抽7人. (12分)
| 20 |
| n |
得n=100人;(3分)
(2)由题意y=3的学生总人数为100-(7+20+5+9+18+6)=35,
设应在y=3的学生抽m人,则
| 20 |
| 100 |
| m |
| 35 |
(3)由题意可知a+b=35-4=31人,且a≥9,b≥2,
满足条件的(a,b)有(9,22),(10,21),(29,2),
共有21组,其中b>a的有7组. (9分)
记C表示时间“项目A得(3分)的人数比得(4分)人数多”
则P(C)=
| 7 |
| 21 |
| 1 |
| 3 |
答:(1)n=100人,(2)则y=3的学生中应抽7人. (12分)
点评:本题属于统计内容,考查分析频数分布直方图和频率的求法.解本题要懂得频率分布直分图的意义,了解频率分布直分图是一种以频数为纵向指标的条形统计图.

练习册系列答案
相关题目
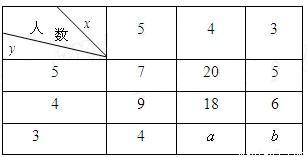 已知某职业技能培训班学生的项目A与项目B成绩抽样统计表如下,抽出学生n人,成绩只有3、4、5三种分值,设x,y分别表示项目A与项目B成绩.例如:表中项目A成绩为5分的共7+9+4=20人.已知x=4且y=5的概率是0.2.
已知某职业技能培训班学生的项目A与项目B成绩抽样统计表如下,抽出学生n人,成绩只有3、4、5三种分值,设x,y分别表示项目A与项目B成绩.例如:表中项目A成绩为5分的共7+9+4=20人.已知x=4且y=5的概率是0.2.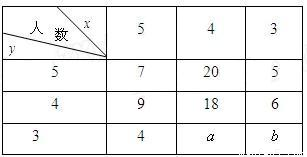 已知某职业技能培训班学生的项目A与项目B成绩抽样统计表如下,抽出学生n人,成绩只有3、4、5三种分值,设x,y分别表示项目A与项目B成绩.例如:表中项目A成绩为5分的共7+9+4=20人.已知x=4且y=5的概率是0.2.
已知某职业技能培训班学生的项目A与项目B成绩抽样统计表如下,抽出学生n人,成绩只有3、4、5三种分值,设x,y分别表示项目A与项目B成绩.例如:表中项目A成绩为5分的共7+9+4=20人.已知x=4且y=5的概率是0.2.