题目内容
给出下列命题:
①过点P(2,1)的抛物线的标准方程是 ;
;
②双曲线 与椭圆
与椭圆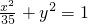 有相同的焦点;
有相同的焦点;
③焦点在x轴上的双曲线C,若离心率为 ,则双曲线C的一条渐近线方程为y=2x.
,则双曲线C的一条渐近线方程为y=2x.
④椭圆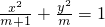 的两个焦点为F1,F2,P为椭圆上的动点,△PF1F2的面积的最大值为2,则m的值为2.其中真命题的序号为________.(写出所有真命题的序号)
的两个焦点为F1,F2,P为椭圆上的动点,△PF1F2的面积的最大值为2,则m的值为2.其中真命题的序号为________.(写出所有真命题的序号)
②③
分析:①过点P(2,1)的抛物线的标准方程是 ,用待定系数法求出抛物线的方程,对比判断;
,用待定系数法求出抛物线的方程,对比判断;
②双曲线 与椭圆
与椭圆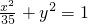 有相同的焦点,求出焦点坐标判断;
有相同的焦点,求出焦点坐标判断;
③焦点在x轴上的双曲线C,若离心率为 ,则双曲线C的一条渐近线方程为y=2x,由题设条件求出渐近线方程.
,则双曲线C的一条渐近线方程为y=2x,由题设条件求出渐近线方程.
④椭圆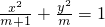 的两个焦点为F1,F2,P为椭圆上的动点,△PF1F2的面积的最大值为2,则m的值为2,由椭圆的简单性质判断.
的两个焦点为F1,F2,P为椭圆上的动点,△PF1F2的面积的最大值为2,则m的值为2,由椭圆的简单性质判断.
解答:①过点P(2,1)的抛物线的标准方程是 是错误命题,因为还有一条焦点在y轴上的抛物线;
是错误命题,因为还有一条焦点在y轴上的抛物线;
②双曲线 与椭圆
与椭圆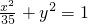 有相同的焦点,是正确命题,因为两个曲线的焦点都在x轴上,半焦距c相等都是
有相同的焦点,是正确命题,因为两个曲线的焦点都在x轴上,半焦距c相等都是 ;
;
③焦点在x轴上的双曲线C,若离心率为 ,则双曲线C的一条渐近线方程为y=2x,是正确命题,因为离心率为
,则双曲线C的一条渐近线方程为y=2x,是正确命题,因为离心率为 解得其渐近线方程为y=±2x,故正确.
解得其渐近线方程为y=±2x,故正确.
④椭圆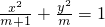 的两个焦点为F1,F2,P为椭圆上的动点,△PF1F2的面积的最大值为2,则m的值为2是错误命题,这是因为,由解析式知,半焦距长为1,,△PF1F2的面积的最大值为2,即bc=2.可得b=2,故m=4,
的两个焦点为F1,F2,P为椭圆上的动点,△PF1F2的面积的最大值为2,则m的值为2是错误命题,这是因为,由解析式知,半焦距长为1,,△PF1F2的面积的最大值为2,即bc=2.可得b=2,故m=4,
综上,正确命题是②③
故答案为:②③.
点评:本题考查圆锥曲线的共同特征,解题的关键是熟练掌握圆锥曲线的性质,并能根据它们的性质进行推理判断,得出结论.
分析:①过点P(2,1)的抛物线的标准方程是
 ,用待定系数法求出抛物线的方程,对比判断;
,用待定系数法求出抛物线的方程,对比判断;②双曲线
 与椭圆
与椭圆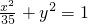 有相同的焦点,求出焦点坐标判断;
有相同的焦点,求出焦点坐标判断;③焦点在x轴上的双曲线C,若离心率为
 ,则双曲线C的一条渐近线方程为y=2x,由题设条件求出渐近线方程.
,则双曲线C的一条渐近线方程为y=2x,由题设条件求出渐近线方程.④椭圆
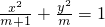 的两个焦点为F1,F2,P为椭圆上的动点,△PF1F2的面积的最大值为2,则m的值为2,由椭圆的简单性质判断.
的两个焦点为F1,F2,P为椭圆上的动点,△PF1F2的面积的最大值为2,则m的值为2,由椭圆的简单性质判断.解答:①过点P(2,1)的抛物线的标准方程是
 是错误命题,因为还有一条焦点在y轴上的抛物线;
是错误命题,因为还有一条焦点在y轴上的抛物线;②双曲线
 与椭圆
与椭圆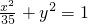 有相同的焦点,是正确命题,因为两个曲线的焦点都在x轴上,半焦距c相等都是
有相同的焦点,是正确命题,因为两个曲线的焦点都在x轴上,半焦距c相等都是 ;
;③焦点在x轴上的双曲线C,若离心率为
 ,则双曲线C的一条渐近线方程为y=2x,是正确命题,因为离心率为
,则双曲线C的一条渐近线方程为y=2x,是正确命题,因为离心率为 解得其渐近线方程为y=±2x,故正确.
解得其渐近线方程为y=±2x,故正确.④椭圆
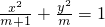 的两个焦点为F1,F2,P为椭圆上的动点,△PF1F2的面积的最大值为2,则m的值为2是错误命题,这是因为,由解析式知,半焦距长为1,,△PF1F2的面积的最大值为2,即bc=2.可得b=2,故m=4,
的两个焦点为F1,F2,P为椭圆上的动点,△PF1F2的面积的最大值为2,则m的值为2是错误命题,这是因为,由解析式知,半焦距长为1,,△PF1F2的面积的最大值为2,即bc=2.可得b=2,故m=4,综上,正确命题是②③
故答案为:②③.
点评:本题考查圆锥曲线的共同特征,解题的关键是熟练掌握圆锥曲线的性质,并能根据它们的性质进行推理判断,得出结论.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 5、如图,M是正方体ABCD-A1B1C1D1的棱DD1的中点,给出下列命题
5、如图,M是正方体ABCD-A1B1C1D1的棱DD1的中点,给出下列命题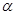 上有不共线的三点到平面
上有不共线的三点到平面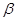 的距离相等,则
的距离相等,则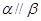 ;(4)若直线
;(4)若直线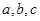 满足
满足 则
则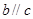 .其中正确命题的个数是 (
)
.其中正确命题的个数是 (
) B.
B.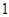 C.
C.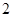 D.
D.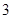
 中,棱长为4,
中,棱长为4, 是BC的中点,
是BC的中点, 在线段
在线段 上运动(
上运动( 、
、
 平面
平面 ,
,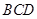 交于点Q,
交于点Q, 面
面
 ②Q点一定在直线DM上 ③
②Q点一定在直线DM上 ③
 中,棱长为4,
中,棱长为4, 是BC的中点,
是BC的中点, 在线段
在线段 上运动(
上运动( 、
、
 平面
平面 ,
, 交于点Q,给出下列命题:
交于点Q,给出下列命题: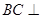 面
面
 ②Q点一定在直线DM上 ③
②Q点一定在直线DM上 ③

 中,棱长为4,
中,棱长为4, 是BC的中点,
是BC的中点, 在线段
在线段 上运动(
上运动( 、
、
 平面
平面 ,
, 交于点Q,
交于点Q, 面
面
 ②Q点一定在直线DM上 ③
②Q点一定在直线DM上 ③